题目内容
14.计算:$\sqrt{5}$($\sqrt{5}$+$\frac{1}{\sqrt{5}}$)=6.分析 根据乘法分配律可以解答本题.
解答 解:$\sqrt{5}$($\sqrt{5}$+$\frac{1}{\sqrt{5}}$)
=5+1
=6,
故答案为:6.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式的混合运算的计算方法.

练习册系列答案
相关题目
6.10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm)如表所示:
设两队队员身高的平均数依次为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,身高的方差依次为${S}_{甲}^{2}$,${S}_{乙}^{2}$,则下列关系中完全正确的是( )
| 队员1 | 队员2 | 队员3 | 队员4 | 队员5 | |
| 甲队 | 173 | 175 | 175 | 175 | 177 |
| 乙队 | 170 | 171 | 175 | 179 | 180 |
| A. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${S}_{甲}^{2}$>${S}_{乙}^{2}$ | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${S}_{甲}^{2}$<${S}_{乙}^{2}$ | ||
| C. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,${S}_{甲}^{2}$>${S}_{乙}^{2}$ | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,${S}_{甲}^{2}$<${S}_{乙}^{2}$ |
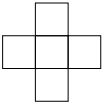
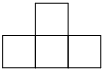
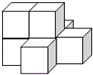 如图是一个由7个同样的立方体叠成的几何体,请问下列选项中,既是中心对称图形,又是这个几何体的三视图之一的是( )
如图是一个由7个同样的立方体叠成的几何体,请问下列选项中,既是中心对称图形,又是这个几何体的三视图之一的是( )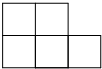

 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论: