题目内容
5.(1)如图①,求证:∠A+∠B=∠C+∠D.(2)如图②,求证:∠A+∠B+∠C=∠BDC.
(3)如图③,则:∠A+∠B+∠C+∠D+∠E=180°.
(4)如图④,则:∠A+∠B+∠C+∠D+∠E+∠F=360°.
(5)如图⑤,则:∠A+∠B+∠C+∠D+∠E=180°.
(6)如图⑥,则:∠A+∠B+∠C+∠D+∠E+∠F=360°.
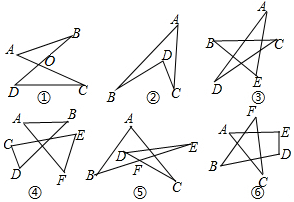
分析 ①根据三角形内角和定理、对顶角相等的性质即可求解;
②连结AD并且延长至E,根据三角形外角的性质即可求解;
③根据三角形外角的性质和三角形内角和定理即可求解;
④根据三角形外角的性质即可求解;
⑤根据三角形外角的性质和三角形内角和定理即可求解;
⑥根据三角形外角的性质和四边形内角和定理即可求解.
解答  (1)证明:如图①,∵∠A+∠B+∠1=∠C+∠D+∠2,∠1=∠2,
(1)证明:如图①,∵∠A+∠B+∠1=∠C+∠D+∠2,∠1=∠2,
∴∠A+∠B=∠C+∠D.
(2)证明:如图②,连结AD并且延长至E,
∵∠1=∠B+∠3,∠2=∠C+∠4,
∴∠A+∠B+∠C=∠BDC.
(3)解:如图③,∵∠1=∠C+∠D,∠2=∠B+∠E,
∴∠A+∠B+∠C+∠D+∠E=180°.
(4)解:如图④,∵∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠1+∠2+∠3=360°.
(5)解:如图⑤,∵∠1=∠2+∠C,∠2=∠E+∠D,
∴∠A+∠B+∠C+∠D+∠E=∠A+∠B+∠1=180°.
(6)解:如图⑥,∵∠1=∠2+∠C,∠2=∠B+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠A+∠1+∠D+∠E=360°.
故答案为:180°;360°;180°;360°.
点评 本题考查三角形外角的性质及三角形、四边形的内角和定理,解答的关键是沟通外角和内角的关系.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
20. 如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
(1)填表:
(2)如果剪了100次,共剪出多少个小正方形?
(3)如果剪n次,共剪出多少个小正方形?
(4)如果要剪出100个正方形,那么需要剪多少次?
 如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
如图,将一张正方形纸片剪去四个大小形状一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中一个小正方形剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.(1)填表:
| 剪的次数 | 1 | 2 | 3 | 4 | 5 |
| 正方形个数 | 4 | 7 | 10 | 13 | 16 |
(3)如果剪n次,共剪出多少个小正方形?
(4)如果要剪出100个正方形,那么需要剪多少次?
10.用两根长为48cm的铁丝分别围成一个长和宽之比为2:1的长方形和一个正方形,则长方形和正方形的面积依次为( )cm2.
| A. | 24和12 | B. | 12和24 | C. | 128和144 | D. | 144和128 |
17. 如图,∠A+∠B+∠C+∠D+∠E的度数为( )
如图,∠A+∠B+∠C+∠D+∠E的度数为( )
 如图,∠A+∠B+∠C+∠D+∠E的度数为( )
如图,∠A+∠B+∠C+∠D+∠E的度数为( )| A. | 180o | B. | 270o | C. | 360o | D. | 540o |
15.一木工师傅有两根长分别为80cm、150cm的木条,他要找第三根木条,将它们钉成一个三角形框架,他可以选择长为( )的木条.
| A. | 70cm | B. | 105cm | C. | 230cm | D. | 300 |