Question

4．平行四边形ABCD的两条对角线AC、BD相交于点O，AB=$\sqrt{5}$，AO=2，OB=1．四边形ABCD是菱形吗？为什么？

Answer 1

分析 在△AOB中，根据勾股定理可证△AOB为直角三角形，即可证AC、BD互相垂直．根据菱形的判定，即对角线互相垂直的平行四边形是菱形，可证四边形ABCD是菱形．

解答 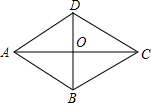解：在△AOB中，
∵AB=$\sqrt{5}$，AO=2，OB=1，
∴AB²=（$\sqrt{5}$）²=5，AO²+OB²=2²+1²=5，
∴AB²=AO²+OB²，
∴△AOB为直角三角形，即∠AOB=90°．
∴AC、BD互相垂直．
∴四边形ABCD是菱形（对角线互相垂直的平行四边形是菱形）．

点评 本题考查了勾股定理和平行四边形的性质以及菱形的判定，菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：①定义；②四边相等；③对角线互相垂直平分．