题目内容
19.如图的数轴上有两处不小心被墨水淹没了,所标注的数据是墨水部分边界与数轴相交点的数据;则被淹没的整数点有69个,负整数点有52 个,被淹没的最小的负整数点所表示的数是-72.
分析 根据数轴的构成可知,-72$\frac{1}{2}$和-41$\frac{1}{5}$之间的整数点有:-72,-71,…,-41,共32个;-21$\frac{3}{4}$和16$\frac{2}{3}$之间的整数点有:-21,-20,…,16,共38个;依此即可求解.
解答 解:由数轴可知,
-72$\frac{1}{2}$和-41$\frac{1}{5}$之间的整数点有:-72,-71,…,-42,共31个;-21$\frac{3}{4}$和16$\frac{2}{3}$之间的整数点有:-21,-20,…,16,共38个;
故被淹没的整数点有31+38=69个,负整数点有31+21=52个,被淹没的最小的负整数点所表示的数是-72.
故答案为:69,52,-72.
点评 本题考查了数轴,熟悉数轴的结构是解题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
14.某种产品的成本是120元/件,试销阶段每件产品的售价x(元)与产品的日销量y(件)之间关系如表所示:
若日销售量y是销售价x的一次函数,那么,要使每天所获得最大的利润,每件产品的销售价应定为多少元?此时每天的销售利润是多少?
| x/元 | 130 | 150 | 165 |
| y/件 | 70 | 50 | 35 |
9.以4、9为两边长的三角形的第三边长是方程x2-14x+40=0的根,则这个三角形的周长为( )
| A. | 17或23 | B. | 17 | C. | 23 | D. | 以上都不对 |
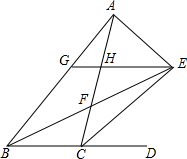 如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论: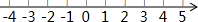
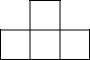 某几何体由若干个大小相同的正方体搭建而成,其主(正)视图、左(侧)视图相同,如图所示,则构成这个几何体至少需要几个正方体( )
某几何体由若干个大小相同的正方体搭建而成,其主(正)视图、左(侧)视图相同,如图所示,则构成这个几何体至少需要几个正方体( )