题目内容
18.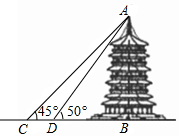 某中学九年级数学兴趣小组想测量建筑物AB的高度,他们在C处仰望建筑物顶端A,测得仰角为45°,再往建筑物的方向前进3.8米到达D处,测得仰角为50°,AB⊥CB,求建筑物的高度.(测角器的高度忽略不计,结果保留小数点后一位,参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
某中学九年级数学兴趣小组想测量建筑物AB的高度,他们在C处仰望建筑物顶端A,测得仰角为45°,再往建筑物的方向前进3.8米到达D处,测得仰角为50°,AB⊥CB,求建筑物的高度.(测角器的高度忽略不计,结果保留小数点后一位,参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
分析 Rt△ADB中用AB表示出BD、Rt△ACB中用AB表示出BC,根据CD=BC-BD可得关于AB 的方程,解方程可得.
解答 解:∵AB⊥BC,∠ACB=45°,
∴AB=CB,
∴AB=3.8+BD,
在Rt△ADB中,tan∠ADB=$\frac{AB}{DB}$,即tan50°=$\frac{3.8+BD}{BD}$=1.19,
∴BD=20,
∴AB=20+3.8=23.8米,
答:建筑物的高度是23.8米.
点评 本题考查解直角三角形的应用-仰角俯角问题,解题的关键是利用数形结合的思想找出各边之间的关系,然后找出所求问题需要的条件.

练习册系列答案
相关题目
8.下列方程中,解为x=-3的是( )
| A. | $\frac{1}{3}$x+1=0 | B. | 2x-1=8-x | C. | -3x=1 | D. | x+$\frac{1}{3}$=0 |
9.先化简后求值.
已知x:y=2:3,求($\frac{{x}^{2}-{y}^{2}}{xy}$)÷[(x+y)•($\frac{x-y}{x}$)3]÷$\frac{x}{{y}^{2}}$的值.
已知x:y=2:3,求($\frac{{x}^{2}-{y}^{2}}{xy}$)÷[(x+y)•($\frac{x-y}{x}$)3]÷$\frac{x}{{y}^{2}}$的值.
7.下列各式中运算正确的是( )
| A. | 2a2+5a3=7a5 | B. | 7t-t=6 | C. | 2x+3y=5xy | D. | 2x2y-2yx2=0 |
8.一个口袋中有2个红球,3个白球,这些球除色外都相同,从口袋中随机摸出一个球,这个球是白球的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{2}$ |