题目内容
13.在平面直角坐标系中,A(a,0),B(4,b),且a、b满足$\sqrt{a-2}$+$\sqrt{b-3}$=0,(1)填空:a=2,b=3;
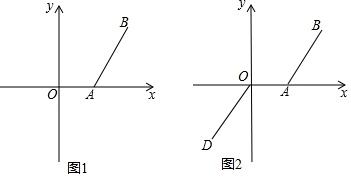
(2)如图1,在x轴上有点C,当S△ABC=6时,求C点坐标;
(3)如图2,将线段BA平移到线段OD,P(n,-1)是线段OD上的一点,求n的值.
分析 (1)根据非负数的性质列方程求解即可;
(2)根据点B的坐标求出点B到x轴的距离,再利用三角形的面积求出AC的长度,然后分点C在点A的左边与右边两种情况讨论求解;
(3)根据平移求出点D的坐标,然后求出直线OD的解析式,再将点P的坐标代入求解即可.
解答 解:(1)由题意得,a-2=0,b-3=0,
解得a=2,b=3;
故答案为:2,3;
(2)∵点B的坐标为(4,3),点A、C都在x轴上,
∴点B到AC的距离为3,
∴S△ABC=$\frac{1}{2}$×AC•3=6,
解得AC=4,
若点C在点A的左边,则2-4=-2,
若点C在点A的右边,则2+4=6,
所以,点C的坐标为(-2,0)或(6,0);
(3)∵点B(4,3)平移到O(0,0),
∴点A平移到D(-2,-3),
∴直线OD的解析式为y=$\frac{3}{2}$x,
∵P(n,-1)是线段OD上的一点,
∴$\frac{3}{2}$n=-1,
解得n=-$\frac{2}{3}$.
点评 本题考查了坐标与图形变化-平移,非负数的性质,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.

练习册系列答案
相关题目
 如图,若灯塔在货轮的南偏东50°,40nmile处,则货轮在灯塔的北偏西50°,40nmile处.
如图,若灯塔在货轮的南偏东50°,40nmile处,则货轮在灯塔的北偏西50°,40nmile处.
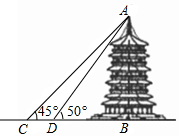 某中学九年级数学兴趣小组想测量建筑物AB的高度,他们在C处仰望建筑物顶端A,测得仰角为45°,再往建筑物的方向前进3.8米到达D处,测得仰角为50°,AB⊥CB,求建筑物的高度.(测角器的高度忽略不计,结果保留小数点后一位,参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
某中学九年级数学兴趣小组想测量建筑物AB的高度,他们在C处仰望建筑物顶端A,测得仰角为45°,再往建筑物的方向前进3.8米到达D处,测得仰角为50°,AB⊥CB,求建筑物的高度.(测角器的高度忽略不计,结果保留小数点后一位,参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19) 如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.