题目内容
9．先化简后求值．已知x：y=2：3，求（$\frac{{x}^{2}-{y}^{2}}{xy}$）÷[（x+y）•（$\frac{x-y}{x}$）3]÷$\frac{x}{{y}^{2}}$的值．
分析 首先把分式的分子和分母分解因式，把除法转化为乘法，计算乘法即可化简，然后根据x：y=2：3，则设x=2m，则y=3m，代入所求的式子进行化简即可．
解答 解：原式=$\frac{（x+y）（x-y）}{xy}$÷$\frac{（x+y）（x-y）^{3}}{{x}^{3}}$÷$\frac{x}{{y}^{2}}$
=$\frac{（x+y）（x-y）}{xy}$•$\frac{{x}^{3}}{（x+y）（x-y）^{3}}$•$\frac{{y}^{2}}{x}$
=$\frac{xy}{（x-y）^{2}}$，
∵x：y=2：3，
∴设x=2m，则y=3m，
则原式=$\frac{6{m}^{2}}{{m}^{2}}$=6．
点评 本题考查了分式的化简求值以及二次根式的化简，正确把分式的分子和分母分解因式是本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
17．下列各式计算正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | 2+$\sqrt{2}$=2$\sqrt{2}$ | C． | $\sqrt{12}$-$\sqrt{10}$=$\sqrt{2}$ | D． | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ |
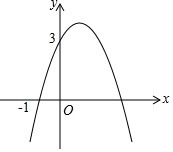已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．
如图，若灯塔在货轮的南偏东50°，40nmile处，则货轮在灯塔的北偏西50°，40nmile处．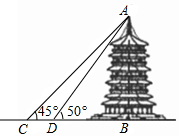
某中学九年级数学兴趣小组想测量建筑物AB的高度，他们在C处仰望建筑物顶端A，测得仰角为45°，再往建筑物的方向前进3.8米到达D处，测得仰角为50°，AB⊥CB，求建筑物的高度．（测角器的高度忽略不计，结果保留小数点后一位，参考数据sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）