题目内容
14. 如图,在平面直角坐标系中,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,点C在x轴上,若四边形OABC为平行四边形,则四边形OABC的面积为6.
如图,在平面直角坐标系中,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,点C在x轴上,若四边形OABC为平行四边形,则四边形OABC的面积为6.
分析 首先设A(a,b),B(x,b),根据反比例函数关系式求出a与x的关系,从而得到AB=CO的长,再利用平行四边形面积公式算出面积即可.
解答 解:过A作AE⊥x轴于点E,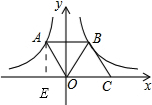
设A(a,b),B(x,b),
∵点A在反比例函数y=-$\frac{2}{x}$上,点B在反比例函数y=$\frac{4}{x}$(x>0)上,
∴ab=-2,xb=4,
∴x=-2a,
∴AB=|-2a-a|=3a,
∵四边形OABC是平行四边形,
∴CO=AB=3a,
∴四边形OABC的面积是:CO•BE=6ab=6,
故答案是:6.
点评 此题主要考查了反比例函数,关键是利用反比例函数关系式表示出A、B两点的坐标,求出CO的长.

练习册系列答案
相关题目
2.从0,1,2,3,4,5,6这七个数中,随机抽取一个数,记为a,若a使关于x的不等式组$\left\{\begin{array}{l}x+5<5x+1\\ x-a>-4\end{array}$的解集为x>1,且使关于x的分式方程$\frac{ax-6}{x-2}$=2的解为非负数,那么取到满足条件的a值的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
3.下列说法错误的是( )
| A. | 三边相等的三角形是等边三角形 | |
| B. | 三个内角都相等的三角形是等边三角形 | |
| C. | 顶角是60°的等腰三角形是等边三角形 | |
| D. | 等腰三角形一腰上的高与另一腰成30°角,则这个三角形是等边三角形 |