题目内容
16.结合具体的数的运算,归纳有关特例,然后比较下列数的大小:(1)小于1的正数a,a的平方,a的立方;
(2)大于-1的负数b,b的平方,b的立方.
分析 (1)根据$\frac{1}{2}$的平方、立方,有理数的大小比较,可得答案;
(2)根据(-$\frac{1}{2}$)的平方、立方,有理数的大小比较,可得答案.
解答 解:(1)a=$\frac{1}{2}$时,a2=$\frac{1}{4}$,a3=$\frac{1}{8}$,
当0<a<1时,a>a2>a3;
(2)a=-$\frac{1}{2}$时,a2=$\frac{1}{4}$,a3=-$\frac{1}{8}$,
当-1<a<0时,a<a3<a2.
点评 本题考查了有理数的大小比较,利用特殊值法得出规律是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.若a2-$\sqrt{22}$a+1=0,则a-$\frac{1}{a}$的值是( )
| A. | ±2$\sqrt{3}$ | B. | ±3$\sqrt{2}$ | C. | ±4$\sqrt{3}$ | D. | ±6$\sqrt{2}$ |
8. 有一个数值转换器,原理如下:当输入的x=81时,输出的y等于( )
有一个数值转换器,原理如下:当输入的x=81时,输出的y等于( )
 有一个数值转换器,原理如下:当输入的x=81时,输出的y等于( )
有一个数值转换器,原理如下:当输入的x=81时,输出的y等于( )| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
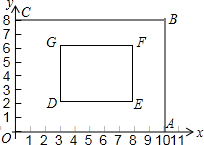 如图,矩形OABC∽矩形DEFG,相似比为2,已知点A(10,0),C(0,8),D(3,2).
如图,矩形OABC∽矩形DEFG,相似比为2,已知点A(10,0),C(0,8),D(3,2).