Question

7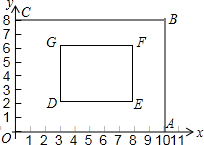．如图，矩形OABC∽矩形DEFG，相似比为2，已知点A（10，0），C（0，8），D（3，2）．
（1）求B，E，F，G各点坐标；
（2）判断G，E是否在直线AC上．

Answer 1

分析 （1）根据相似多边形的性质求出DE和DG的长，确定各点坐标；
（2）运用待定系数法求出直线AC的解析式，把点G，E的坐标代入解析式判断即可．

解答 解：（1）由题意得，OA=10，OC=8，
∵矩形OABC∽矩形DEFG，相似比为2，
∴DE=$\frac{1}{2}$OA=5，DG=$\frac{1}{2}$OC=4，
∴B（10，8），E（8，2），F（8，6），G（3，6）；
（2）设直线AC的解析式为y=kx+b，
则$\left\{\begin{array}{l}{10k+b=0}\\{b=8}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=-\frac{4}{5}}\\{b=8}\end{array}\right.$，
故直线AC的解析式为y=-$\frac{4}{5}$x+8，
G，E的坐标不满足直线AC的解析式，
故G，E不在直线AC上．

点评 本题考查的是相似多边形的性质、坐标与图形的性质、待定系数法求一次函数解析式，掌握相似多边形对应边成比例是解题的关键．