题目内容
20.已知:直线l平行于直线y=2x+m,且与直线y=-x-8的交点的横坐标为2,则直线l的函数表达式是y=2x-14.分析 由直线l平行于直线y=2x+m,得出k=2,直线y=-x-8的交点的横坐标为2,得出交点坐标为(2,-10),设直线l的函数表达式y=kx+b,代入k和交点坐标求得答案即可.
解答 解:设直线l的函数表达式y=kx+b,
∵直线l平行于直线y=2x+m,
∴k=2,
∵与直线y=-x-8的交点的横坐标为2,
∴交点坐标为(2,-10),
则-10=2×2+b,
解得:b=-14,
因此直线l的函数表达式是y=2x-14.
故答案为:y=2x-14.
点评 本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
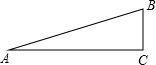 如图,在Rt△ABC中,∠C=90°,∠A=15°
如图,在Rt△ABC中,∠C=90°,∠A=15°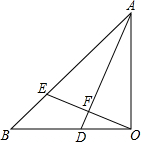 如图,△AOB中,OB=OA,∠AOB=90°,AD平分∠OAB交OB于D,OE⊥AD交AB于E,垂足为F,下列结论:
如图,△AOB中,OB=OA,∠AOB=90°,AD平分∠OAB交OB于D,OE⊥AD交AB于E,垂足为F,下列结论: