题目内容
2．
如图，已知在△ABC中，∠C=90°，AB的垂直平分线交BC于D，垂足为E，∠CAD：∠DAB=2：1，求∠BAC的度数．
分析 根据线段的垂直平分线的性质得到DA=DB，得到∠DAB=∠B，设∠DAB=x，根据三角形内角和等于180°列出方程，解方程得到答案．
解答 解：∵DE是AB的垂直平分线，
∴DA=DB，
∴∠DAB=∠B，
设∠DAB=x，则∠B=x，∠CAD=2x，
由题意得，x+x+2x=90°，
解得x=22.5°，
则∠BAC=x+2x=67.5°．
点评 此题主要考查线段的垂直平分线的性质，线段的垂直平分线上的点到线段的两个端点的距离相等．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知四边形ABCD值，AB∥GH∥CD，AB=20，CD=8，DG：GA=3：2，求GH的长．
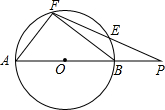如图，点P在⊙O的直径AB的延长线上，PEF是⊙O的割线，且AF=FE，$\frac{PB}{PE}=\frac{5}{6}$，△ABF的面积为96．
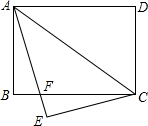如图，矩形ABCD中，AB=6，BC=8，将△ACD沿对角线AC翻折得△ACE，AE交BC于点F，将△CEF绕点C逆时针旋转α角（0°＜α＜180°）得△CE′F′，点E、F的对应点分别为E、F的对应点分别为E′、F′．旋转过程中直线CF′、E′F′分别交直线AE于点M、N，当△F′NM是等腰三角形且MN=MF′时，则MN=$\frac{275}{56}$．
5．设a=-（-3-2）2，b=（-3）×（-2），c=（-3）2÷（-2）2，则（ ）
| A． | b＞a＞c | B． | b＞c＞a | C． | a＞b＞c | D． | c＞a＞b |
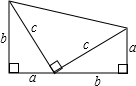利用如图来证明勾股定理．