题目内容
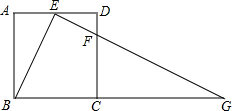 如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=
如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=| 1 |
| 4 |
(1)求证:△ABE∽△DEF;
(2)若正方形ABCD的边长为8,求BG的长.
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:(1)证明∠A=∠D=90°;证明
=
,结合∠A=∠D,得到△ABE∽△DEF.
(2)证明△DEF∽△CGF,得到
=
;结合DE=4,DF=
DC,求出CG的长度,即可解决问题.
| AE |
| DF |
| AB |
| DE |
(2)证明△DEF∽△CGF,得到
| ED |
| CG |
| DF |
| CF |
| 1 |
| 4 |
解答: (1)证明:∵四边形ABCD为正方形,
(1)证明:∵四边形ABCD为正方形,
∴AD=DC=BC=AB,∠A=∠D=90°,
∵AE=DE,
∴
=
;
又∵DF=
DC,
∴
=
;
∴
=
,即
=
;
∵∠A=∠D,
∴△ABE∽△DEF.
(2)解:∵四边形ABCD为正方形,
∴ED∥CG,
∴△DEF∽△CGF,
∴
=
;
又∵DF=
DC,正方形的边长为8,
∴ED=4,CG=12,
∴BG=BC+CG=20.
 (1)证明:∵四边形ABCD为正方形,
(1)证明:∵四边形ABCD为正方形,∴AD=DC=BC=AB,∠A=∠D=90°,
∵AE=DE,
∴
| AE |
| AB |
| 1 |
| 2 |
又∵DF=
| 1 |
| 4 |
∴
| DF |
| DE |
| 1 |
| 2 |
∴
| AE |
| AB |
| DF |
| DE |
| AE |
| DF |
| AB |
| DE |
∵∠A=∠D,
∴△ABE∽△DEF.
(2)解:∵四边形ABCD为正方形,
∴ED∥CG,
∴△DEF∽△CGF,
∴
| ED |
| CG |
| DF |
| CF |
又∵DF=
| 1 |
| 4 |
∴ED=4,CG=12,
∴BG=BC+CG=20.
点评:该题主要考查了正方形的性质、相似三角形的判定及其性质等几何知识点及其应用问题;解题的关键是牢固掌握正方形的性质、相似三角形的判定及其性质等几何知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一天有24小时,一小时有60分,一分为60秒.故一天共有86400秒.用科学记数法表示86400为( )
| A、8.64×104 |
| B、8.64×105 |
| C、0.864×105 |
| D、0.864×104 |
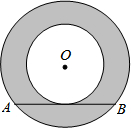 如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=2m,则图中阴影部分的面积是( )
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=2m,则图中阴影部分的面积是( )| A、m2π |
| B、2m2π |
| C、4m2π |
| D、8m2π |
 美化城市,改善人们的居住环境已成为城市建设的一项重要内容,某市城区近几年来,通过拆旧房.植草,栽树,修建公园等设施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容,某市城区近几年来,通过拆旧房.植草,栽树,修建公园等设施,使城区绿地面积不断增加(如图所示). 某小区有一块长方形草坪,为方便居民穿行和健身,小区管理人员沿草坪对角线修一条长39m的砖路,并在草坪周围铺设了一圈石子路(石子路的宽度忽略不计),如图所示,已知长方形草坪的长与宽之比为3:2,求所铺设的石子路的总长度.(结果精确到0.1,参考数据:
某小区有一块长方形草坪,为方便居民穿行和健身,小区管理人员沿草坪对角线修一条长39m的砖路,并在草坪周围铺设了一圈石子路(石子路的宽度忽略不计),如图所示,已知长方形草坪的长与宽之比为3:2,求所铺设的石子路的总长度.(结果精确到0.1,参考数据: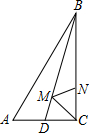 如图△ABC,∠ACB=90°,BC=12,AC=5,AB=13,BD平分∠ABC,M、N分别为BD、BC上的点,则CM+MN的最小值是
如图△ABC,∠ACB=90°,BC=12,AC=5,AB=13,BD平分∠ABC,M、N分别为BD、BC上的点,则CM+MN的最小值是