题目内容
已知AB是⊙O的直径,AD,BC是⊙O的两条切线,DC与⊙O相切于点E,如图1,求证:OD∥BE;如图2,若AD=9,BC=16,求tan∠DBE的值.
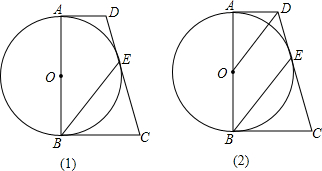
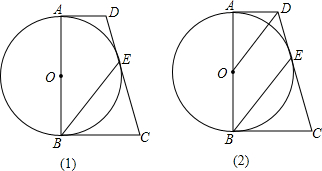
考点:切线的性质
专题:
分析:(1)连接OE,可证明△AOD≌△EOD,结合条件可证明∠AOD=∠OBE,可证得OD∥BE.
(2)作OF⊥BD于F,作DM⊥BC于M;得四边形ADMB是矩形,求出AB、OD、DF、OF的长,再证出∠DBE=∠ODF,即可求出tan∠DBE的值.
(2)作OF⊥BD于F,作DM⊥BC于M;得四边形ADMB是矩形,求出AB、OD、DF、OF的长,再证出∠DBE=∠ODF,即可求出tan∠DBE的值.
解答:解:(1)证明:如图1所示,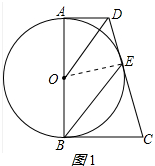 连接OE,
连接OE,
∵DA,DC是⊙O的切线,
∴OA⊥AD,OE⊥CD,且DA=DE,
在Rt△AOD和Rt△EOD中,
,
∴Rt△AOD≌Rt△EOD(HL),
∴∠AOD=∠DOE,
又∵OE=OB,
∴∠OBE=∠OEB,
又∵∠AOE=∠OBE+∠OEB,
即2∠AOD=2∠OBE,
∴∠AOD=∠OBE,
∴OD∥BE.
(2)作OF⊥BD于F,作DM⊥BC于M;如图2所示:
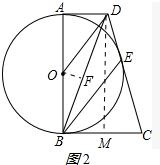 则四边形ADMB是矩形,
则四边形ADMB是矩形,
∴BM=AD=9,DM=AB;
∵AD、BC、CD是⊙O的切线,
∴DE=AD=9,CE=BC=16,∠DAB=90°,
∴CD=16+9=25,CM=16-9=7,
∴DM=
=24,
∴AB=DM=24,OA=12,
∴BD=
=3
,
∵∠OFB=∠DAB=90°,∠OBF=∠DBA,∴△OBF∽△DBA,∴
=
=
,即
=
=
,∴OF=
=
,BF=
=
,∴DF=BD-BF=3
-
=
,
∵OD∥BE,∴∠DBE=∠ODF,
∴tan∠DBE=tan∠ODF=
=
=
.
 连接OE,
连接OE,∵DA,DC是⊙O的切线,
∴OA⊥AD,OE⊥CD,且DA=DE,
在Rt△AOD和Rt△EOD中,
|
∴Rt△AOD≌Rt△EOD(HL),
∴∠AOD=∠DOE,
又∵OE=OB,
∴∠OBE=∠OEB,
又∵∠AOE=∠OBE+∠OEB,
即2∠AOD=2∠OBE,
∴∠AOD=∠OBE,
∴OD∥BE.
(2)作OF⊥BD于F,作DM⊥BC于M;如图2所示:
 则四边形ADMB是矩形,
则四边形ADMB是矩形,∴BM=AD=9,DM=AB;
∵AD、BC、CD是⊙O的切线,
∴DE=AD=9,CE=BC=16,∠DAB=90°,
∴CD=16+9=25,CM=16-9=7,
∴DM=
| 252-72 |
∴AB=DM=24,OA=12,
∴BD=
| 242+92 |
| 73 |
∵∠OFB=∠DAB=90°,∠OBF=∠DBA,∴△OBF∽△DBA,∴
| OF |
| DA |
| OB |
| BD |
| BF |
| AB |
| OF |
| 9 |
| 12 | ||
3
|
| BF |
| 24 |
| 9×12 | ||
3
|
36
| ||
| 73 |
| 24×12 | ||
3
|
96
| ||
| 73 |
| 73 |
96
| ||
| 73 |
123
| ||
| 73 |
∵OD∥BE,∴∠DBE=∠ODF,
∴tan∠DBE=tan∠ODF=
| OF |
| DF |
| 36 |
| 123 |
| 12 |
| 41 |
点评:本题主要考查切线的性质、平行线的判定与性质以及锐角三角函数的运用;主要考查学生综合运用定理进行推理和计算的能力.

练习册系列答案
相关题目
下列各式中,运算正确的是( )
| A、2(a-1)=2a-1 |
| B、a2+a2=2a2 |
| C、2a3-3a3=a3 |
| D、a+a2=a3 |
青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米,将2500000用科学记数法表示应为( )
| A、25×105 |
| B、2.5×106 |
| C、0.25×107 |
| D、2.5×107 |
 如图,线段AD:DE:EF=3:5:3,EF=3cm,求线段AE、AF的长.
如图,线段AD:DE:EF=3:5:3,EF=3cm,求线段AE、AF的长.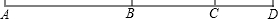 已知:B是线段上AC上一点,且AB:BC=10:7,D是线段AC延长线上一点,且BD:AC=11:17,若CD=16,求BC的长.
已知:B是线段上AC上一点,且AB:BC=10:7,D是线段AC延长线上一点,且BD:AC=11:17,若CD=16,求BC的长.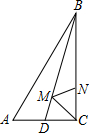 如图△ABC,∠ACB=90°,BC=12,AC=5,AB=13,BD平分∠ABC,M、N分别为BD、BC上的点,则CM+MN的最小值是
如图△ABC,∠ACB=90°,BC=12,AC=5,AB=13,BD平分∠ABC,M、N分别为BD、BC上的点,则CM+MN的最小值是 已知线段AB,延长AB到C,使BC=
已知线段AB,延长AB到C,使BC= 如图,由四个全等的直角三角形及一个小正方形拼成一个大正方形,已知直角三角形的短直角边长为3,小正方形的面积为1,则大正方形的面积为
如图,由四个全等的直角三角形及一个小正方形拼成一个大正方形,已知直角三角形的短直角边长为3,小正方形的面积为1,则大正方形的面积为