题目内容
4.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2m≤0}\\{x+m>2}\end{array}\right.$有解,则m的取值范围为( )| A. | m>$\frac{2}{3}$ | B. | m≤$\frac{2}{3}$ | C. | m>-$\frac{2}{3}$ | D. | m≤-$\frac{2}{3}$ |
分析 首先解不等式,利用m表示出两个不等式的解集,根据不等式组有解即可得到关于m的不等式,从而求解.
解答 解:$\left\{\begin{array}{l}{x-2m≤0①}\\{x+m>2②}\end{array}\right.$
解①得:x≤2m,
解②得:x>2-m,
根据题意得:2m>2-m,
解得:m>$\frac{2}{3}$.
故选A
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
12. 将矩形ABCD沿AE折叠,D点落在F处,若∠CEF=60°,则∠EAB等于( )
将矩形ABCD沿AE折叠,D点落在F处,若∠CEF=60°,则∠EAB等于( )
 将矩形ABCD沿AE折叠,D点落在F处,若∠CEF=60°,则∠EAB等于( )
将矩形ABCD沿AE折叠,D点落在F处,若∠CEF=60°,则∠EAB等于( )| A. | 72° | B. | 60° | C. | 55° | D. | 54° |
19.60°的圆心角所对的弧长是3πcm,则此弧所在圆的半径是( )
| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
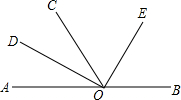 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,请求出∠AOD、∠COE、∠BOC、∠BOE的度数.
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,请求出∠AOD、∠COE、∠BOC、∠BOE的度数.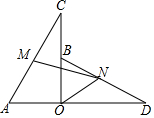 如图,OA=OB,OC=OD,∠AOB=∠COD=90°,M,N分别为AC,BD的中点,连接MN,ON,求证:∠MNO=45°.
如图,OA=OB,OC=OD,∠AOB=∠COD=90°,M,N分别为AC,BD的中点,连接MN,ON,求证:∠MNO=45°.