题目内容
14.解方程(1)5x+3=-7x+9
(2)5(x-1)-2(3x-1)=4x-1
(3)$\frac{3x+1}{2}$=$\frac{7+x}{6}$
(4)$\frac{x}{2}$-$\frac{5x+11}{6}$=1+$\frac{2x-4}{3}$
(5)$\frac{3+0.2x}{0.2}$-$\frac{0.2+0.03x}{0.01}$=0.75.
分析 (1)方程移项合并,把x系数化为1,即可求出解;
(2)方程去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(5)方程整理后,去括号,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)移项合并得:12x=6,
解得:x=0.5;
(2)去括号得:5x-5-6x+2=4x-1,
移项合并得:5x=-2,
解得:x=-0.4;
(3)去分母得:9x+3=7+x,
移项合并得:8x=4,
解得:x=0.5;
(4)去分母得:3x-5x-11=6+4x-8,
移项合并得:6x=-9,
解得:x=-1.5;
(5)方程整理得:15+x-20-3x=0.75,
移项合并得:-2x=5.75,
解得:x=-2.875.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.解方程3x+1=5-x时,下列移项正确的是( )
| A. | 3x+x=5+1 | B. | 3x-x=-5-1 | C. | 1-5=-3x+x | D. | 3x+x=5-1 |
4.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2m≤0}\\{x+m>2}\end{array}\right.$有解,则m的取值范围为( )
| A. | m>$\frac{2}{3}$ | B. | m≤$\frac{2}{3}$ | C. | m>-$\frac{2}{3}$ | D. | m≤-$\frac{2}{3}$ |
 如图,AE是⊙O的直径,B,D是⊙O上的点,AD与EB交于点C,连结AB和DE,过点E的直线与AC的延长线交于点F,且∠F=∠CED=∠AED.
如图,AE是⊙O的直径,B,D是⊙O上的点,AD与EB交于点C,连结AB和DE,过点E的直线与AC的延长线交于点F,且∠F=∠CED=∠AED. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( )
如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( )



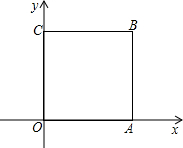 如图所示,正方形OABC的顶点为O(0,0),A(1,0),B(1,1),C(0,1).
如图所示,正方形OABC的顶点为O(0,0),A(1,0),B(1,1),C(0,1).