题目内容
15.先化简,再求值:$\frac{a-3}{{a}^{2}-2a}$÷(a+2-$\frac{5}{a-2}$),其中a是关于x的方程x2+3x-1=0的根.分析 先化简题目中的式子,然后根据a是关于x的方程x2+3x-1=0的根,从而可以解答本题.
解答 解:$\frac{a-3}{{a}^{2}-2a}$÷(a+2-$\frac{5}{a-2}$)
=$\frac{a-3}{a(a-2)}÷\frac{(a+2)(a-2)-5}{a-2}$
=$\frac{a-3}{a(a-2)}×\frac{a-2}{(a+3)(a-3)}$
=$\frac{1}{{a}^{2}+3a}$,
∵a是关于x的方程x2+3x-1=0的根,
∴a2+3a-1=0,
∴a2+3a=1,
∴原式=$\frac{1}{1}$=1.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
4.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2m≤0}\\{x+m>2}\end{array}\right.$有解,则m的取值范围为( )
| A. | m>$\frac{2}{3}$ | B. | m≤$\frac{2}{3}$ | C. | m>-$\frac{2}{3}$ | D. | m≤-$\frac{2}{3}$ |
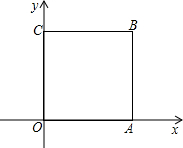 如图所示,正方形OABC的顶点为O(0,0),A(1,0),B(1,1),C(0,1).
如图所示,正方形OABC的顶点为O(0,0),A(1,0),B(1,1),C(0,1).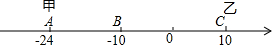 已知数轴上有A、B、C三点,分别代表-24,-10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
已知数轴上有A、B、C三点,分别代表-24,-10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.