题目内容
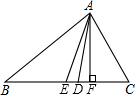 如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则:
如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则:(1)BE=
| 1 |
| 2 |
(2)∠BAD=
| 1 |
| 2 |
(3)∠AFB=
(4)△ABC中,∠B对边是
考点:三角形的角平分线、中线和高
专题:
分析:(1)根据三角形中线的定义进行解答;
(2)根据三角形角平分线的定义进行解答;
(3)根据三角形高的定义进行解答;
(4)根据三角形的定义结合图形解答即可.
(2)根据三角形角平分线的定义进行解答;
(3)根据三角形高的定义进行解答;
(4)根据三角形的定义结合图形解答即可.
解答:解:(1)∵AE是BC边的中线,
∴BE=EC=
BC;
(2)∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=
∠BAC;
(3)∵AF是△ABC边的高,
∴AF⊥BC,
∴∠AFB=∠AFC=90°;
(4))△ABC中,∠B对边是AC,BC所对的角是∠BAC;图中以∠C为内角三角形有 4个,分别为:△ABC、△AEC、△ADC、△AFC.
故答案为:(1)EC;BC;(2)∠CAD;∠BAC;(3)∠AFC;(4)AC;∠BAC;4.
∴BE=EC=
| 1 |
| 2 |
(2)∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=
| 1 |
| 2 |
(3)∵AF是△ABC边的高,
∴AF⊥BC,
∴∠AFB=∠AFC=90°;
(4))△ABC中,∠B对边是AC,BC所对的角是∠BAC;图中以∠C为内角三角形有 4个,分别为:△ABC、△AEC、△ADC、△AFC.
故答案为:(1)EC;BC;(2)∠CAD;∠BAC;(3)∠AFC;(4)AC;∠BAC;4.
点评:此题主要考查了三角形中的重要元素,关键是正确理解三角形的边、三角形的内角、三角形的角平分线、中线、高及三角形的概念.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数y=x2-2015x+2014与x轴交点是(m,0),(n,0),则(m2-2014m+2014)(n2-2014n+2014)的值是( )
| A、2013 | B、2014 |
| C、2015 | D、2016 |
等腰三角形的两个外角的度数比为1:4,则它的底角的度数是( )
| A、140° | B、20° |
| C、60°或140° | D、60° |
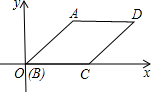 如图,?ABCD放入直角坐标系,BC在x轴上,且AB=4,BC=3,∠ABC=45°,则点D的坐标为
如图,?ABCD放入直角坐标系,BC在x轴上,且AB=4,BC=3,∠ABC=45°,则点D的坐标为 已知四边形OACB的四个顶点分别是O(0,0),B(3,3),C(6,0),A(3,-3).在直角坐标系中画出这个四边形,并求这个四边形的面积.
已知四边形OACB的四个顶点分别是O(0,0),B(3,3),C(6,0),A(3,-3).在直角坐标系中画出这个四边形,并求这个四边形的面积. 欣赏图,请你至少用两种方法分析图中的旋转现象.
欣赏图,请你至少用两种方法分析图中的旋转现象. 四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=3,AB=4,把梯形ABCD分别绕直线
四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=3,AB=4,把梯形ABCD分别绕直线 在△ABC中,点D、E分别是AC、BC边上的点,请你在AB边上确定一点P,使△PDE的周长最小.在图中作出点P.
在△ABC中,点D、E分别是AC、BC边上的点,请你在AB边上确定一点P,使△PDE的周长最小.在图中作出点P.