题目内容
等腰三角形的两个外角的度数比为1:4,则它的底角的度数是( )
| A、140° | B、20° |
| C、60°或140° | D、60° |
考点:等腰三角形的性质
专题:
分析:先设这两个外角等于x,4x,然后分类讨论,①若底角的外角是x;②若顶角的外角是x,再结合三角形内角和定理可求x,从而求解.
解答:解:设这两个外角等于x,4x,
①若底角的外角是x,则有2(180°-x)+(180°-4x)=180°,
解得x=60°,
则底角=120°,不合题意,舍去.
②若顶角的外角是x,则有(180°-x)+2(180°-4x)=180°,
解得x=40°,
则顶角=140°,那么底角=20°.
故选:B.
①若底角的外角是x,则有2(180°-x)+(180°-4x)=180°,
解得x=60°,
则底角=120°,不合题意,舍去.
②若顶角的外角是x,则有(180°-x)+2(180°-4x)=180°,
解得x=40°,
则顶角=140°,那么底角=20°.
故选:B.
点评:本题考查了等腰三角形的性质、三角形内角和定理、分类讨论、三角形外角的定义.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
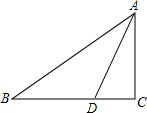 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,CD=4,则点D到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,CD=4,则点D到AB的距离是( )| A、4 | B、2 | C、3 | D、6 |
⊙O1与⊙O2的圆心距为6,且两圆半径是方程x2-6x+5=0的两根,则两圆的位置关系为( )
| A、内切 | B、外切 | C、外离 | D、相交 |
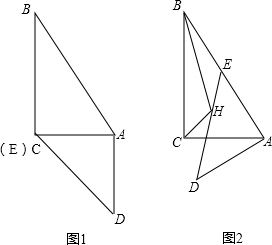 已知如图1,Rt△ABC和Rt△ADE的直角边AC和AE重叠在一起,AD=AE,∠B=30°,∠DAE=∠ACB=90°.
已知如图1,Rt△ABC和Rt△ADE的直角边AC和AE重叠在一起,AD=AE,∠B=30°,∠DAE=∠ACB=90°.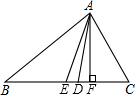 如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则:
如图,在△ABC中,AE是中线,AD是角平分线,AF是高,则: 如图,在平行四边形ABCD中,对角线AC与BD交于点O,作AE⊥BD,CF⊥BD,垂足分别为E、F.则图中全等三角形的对数有( )
如图,在平行四边形ABCD中,对角线AC与BD交于点O,作AE⊥BD,CF⊥BD,垂足分别为E、F.则图中全等三角形的对数有( ) 求出下列图中x的值.
求出下列图中x的值.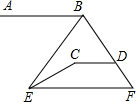 如图,AB∥CD∥EF,若∠ABE=48°,∠ECD=148°.求∠BEC的度数.
如图,AB∥CD∥EF,若∠ABE=48°,∠ECD=148°.求∠BEC的度数.