题目内容
5.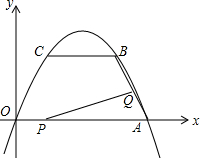 已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.
已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.(1)求这条抛物线的函数关系式;
(2)两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动.其中,点P沿着线段0A向A点运动,点Q沿着线段AB向B点运动.设这两个动点运动的时间为t(秒)(0<t≤2),△PQA的面积记为S.
①求S与t的函数关系式;
②当t为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
③是否存在这样的t值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
分析 (1)运用待定系数法,代入O,A,B,解方程可得a,b,c,进而得到抛物线的方程;
(2)①过B作BE垂直于x轴,过点Q作QF⊥x轴交x轴于F,分别求出PA,QF的长,再由三角形的面积公式,化简即可得到所求;
②由二次函数的最值的求法,即可得到所求最大值及三角形PQA的形状;
③存在,当点Q在AB上运动时,要使得△PQA是直角△,必须使∠PQA=90°.由直角三角形的性质即可得到所求t的值,以及P,Q的坐标.
解答 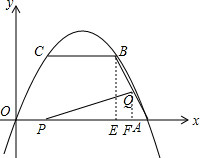 解:(1)抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,
解:(1)抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,
∴$\left\{\begin{array}{l}{16a+4b+c=0}\\{9a+3b+c=3}\end{array}\right.$,
解得a=-$\frac{\sqrt{3}}{3}$,b=$\frac{4\sqrt{3}}{3}$,c=0,
∴y=-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x;
(2)①过B作BE⊥x交x轴于E,则BE=$\sqrt{3}$,AE=1,AB=2,
由tan∠BAE=$\frac{BE}{AE}$=$\sqrt{3}$得∠BAE=60°,
由题意QA=t,PA=4-t,
过点Q作QF⊥x轴交x轴于F,
则sin∠BAE=$\frac{QF}{AQ}$QFAQ,QF=$\frac{\sqrt{3}}{2}$t,
则S=$\frac{1}{2}$PA•QF=$\frac{1}{2}$(4-t)•$\frac{\sqrt{3}}{2}$t=-$\frac{\sqrt{3}}{4}$t2+$\sqrt{3}$t=-$\frac{\sqrt{3}}{4}$(t-2)2+$\sqrt{3}$,
②由=-$\frac{\sqrt{3}}{4}$(t-2)2+$\sqrt{3}$,由-$\frac{\sqrt{3}}{4}$<0,可得当t=2时,S取得最大值$\sqrt{3}$;
此时△PQA是等边三角形;
③存在,当点Q在AB上运动时,
要使得△PQA是直角△,必须使∠PQA=90°.
∴PA=2QA,
∴4-t=2t.
∴t=$\frac{4}{3}$,
∴P($\frac{4}{3}$,0),Q($\frac{10}{3}$,$\frac{2\sqrt{3}}{3}$).
点评 本题考查二次函数的解析式的求法,注意运用待定系数法,考查三角形的面积公式的运用,以及直角三角形的判断,注意运用二次函数的最值的求法,考查运算能力,属于中档题.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案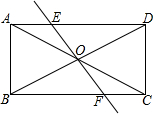 如图.已知矩形ABCD的对角线AC,BD相交于点O,且AD=2AB,过点O的直线与矩形的边AD,BC分别交于两点E、F.随着E、F两点的位置的改变,以A、B、C、D、E、F中的四点为顶点构成的四边形,能构成:①正方形的有2个,②矩形的有2个,③菱形有4个,④平行四边形有无数个.以上四个结论中正确的有(填序号)①③④.
如图.已知矩形ABCD的对角线AC,BD相交于点O,且AD=2AB,过点O的直线与矩形的边AD,BC分别交于两点E、F.随着E、F两点的位置的改变,以A、B、C、D、E、F中的四点为顶点构成的四边形,能构成:①正方形的有2个,②矩形的有2个,③菱形有4个,④平行四边形有无数个.以上四个结论中正确的有(填序号)①③④. 如图,已知∠BOD=110°,求∠A+∠B+∠C+∠D.
如图,已知∠BOD=110°,求∠A+∠B+∠C+∠D.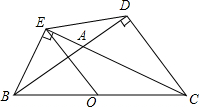 如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于A,∠BAC=120°,求证:DE=OE.
如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于A,∠BAC=120°,求证:DE=OE. 如图,已知正方形ABCD的边长为$\sqrt{5}$,点E,F,G,H分别在正方形的四条边上,且AE=DF=CG=BH,则四边形EFGH的形状为正方形,它的面积的最小值为$\frac{5}{2}$.
如图,已知正方形ABCD的边长为$\sqrt{5}$,点E,F,G,H分别在正方形的四条边上,且AE=DF=CG=BH,则四边形EFGH的形状为正方形,它的面积的最小值为$\frac{5}{2}$.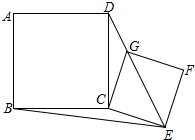 将边长为$\sqrt{5}$的正方形ABCD与边长为$\sqrt{2}$的正方形CEFG如图摆放,点G恰好落在线段DE上.连BE,则BE长为$\sqrt{13}$.
将边长为$\sqrt{5}$的正方形ABCD与边长为$\sqrt{2}$的正方形CEFG如图摆放,点G恰好落在线段DE上.连BE,则BE长为$\sqrt{13}$.