题目内容
17.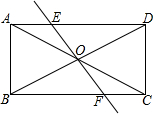 如图.已知矩形ABCD的对角线AC,BD相交于点O,且AD=2AB,过点O的直线与矩形的边AD,BC分别交于两点E、F.随着E、F两点的位置的改变,以A、B、C、D、E、F中的四点为顶点构成的四边形,能构成:①正方形的有2个,②矩形的有2个,③菱形有4个,④平行四边形有无数个.以上四个结论中正确的有(填序号)①③④.
如图.已知矩形ABCD的对角线AC,BD相交于点O,且AD=2AB,过点O的直线与矩形的边AD,BC分别交于两点E、F.随着E、F两点的位置的改变,以A、B、C、D、E、F中的四点为顶点构成的四边形,能构成:①正方形的有2个,②矩形的有2个,③菱形有4个,④平行四边形有无数个.以上四个结论中正确的有(填序号)①③④.
分析 当点E是AD中点或AB中点时,即可判断正方形、矩形、菱形的个数,从而得到答案.
解答 解:图1中,因为AD=2AB,当AE=ED时,四边形ABFE、四边形EFCD是正方形,故能够形成两个正方形①正确,
四边形AFCE、四边形EBFD是菱形,故③正确(包括前面两个正方形).
由图1、图2可知能够形成5个矩形故②错误,
当点E不是中点时,四边形AFCE是平行四边形,
所以平行四边形有无数个,故④正确.
故答案为①③④.

点评 本题考查矩形、正方形、菱形、平行四边形的判定,从特殊位置思考问题,是解决问题的关键,记住正方形既是特殊的菱形也是特殊的矩形,这个是易错的地方.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
5.设函数y=x2+2kx+k-1(k为常数),下列说法正确的是( )
| A. | 对任意实数k,函数与x轴都没有交点 | |
| B. | 存在实数n,满足当x≥n时,函数y的值都随x的增大而减小 | |
| C. | k取不同的值时,二次函数y的顶点始终在同一条直线上 | |
| D. | 对任意实数k,抛物线y=x2+2kx+k-1都必定经过唯一定点 |
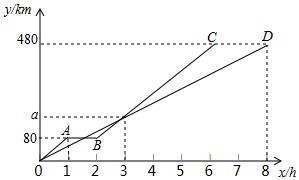 甲、乙两地相距480km,客车、货车同时从甲地出发去乙地,贷车匀速行驶,客车途中停车检修1h,然后提高速度匀速行驶.图中折线OA-AB-BC、线段OD分别表示客车、货车所行驶路程y km与时间x h之间的函数图象.
甲、乙两地相距480km,客车、货车同时从甲地出发去乙地,贷车匀速行驶,客车途中停车检修1h,然后提高速度匀速行驶.图中折线OA-AB-BC、线段OD分别表示客车、货车所行驶路程y km与时间x h之间的函数图象.
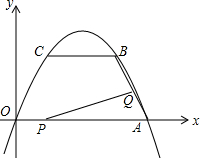 已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.
已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.