题目内容
10.已知n为正整数,且两组数x1,x2,…,xn和y1,y2,…,yn的平均数分别是4和18.(1)若x1,x2,x3的平均数是4,y1,y2,y3,y4的平均数是18,求x1,x2,x3,y1,y2,y3,y4的平均数.
(2)求一组新数据6x1,6x2,…,6xn的平均数.
(3)求一组新数据mx1+ky1,mx2+ky2,…,mxn+kyn的平均数.
分析 (1)根据题意,可得x1+x2+x3=12、y1+y2+y3+y4=72,计算x1,x2,x3,y1,y2,y3,y4的平均数根据公式计算即可;
(2)由题意知,x1+x2+…+xn=4n,代入到新数据6x1,6x2,…,6xn的平均数计算公式中计算即可;
(3)由题意知y1+y2+…+yn=18n,代入到新数据平均数=$\frac{m{x}_{1}+k{y}_{1}+m{x}_{2}+k{y}_{2}+…+m{x}_{n}+k{y}_{n}}{n}$=$\frac{m({x}_{1}+{x}_{2}+…+{x}_{n})+k({y}_{1}+{y}_{2}+…+{y}_{n})}{n}$可得.
解答 解:(1)∵x1,x2,x3的平均数是4,∴x1+x2+x3=4×3=12,
∵y1,y2,y3,y4的平均数是18,∴y1+y2+y3+y4=18×4=72,
x1,x2,x3,y1,y2,y3,y4的平均数=$\frac{{x}_{1}+{x}_{2}+{x}_{3}+{y}_{1}+{y}_{2}+{y}_{3}+{y}_{4}}{7}$=$\frac{12+72}{7}$=12;
(2)∵x1,x2,…,xn的平均数是4,
∴x1+x2+…+xn=4n,
则6x1,6x2,…,6xn的平均数=6×$\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$=6×4=24;
(3)∵y1,y2,…,yn的平均数是18,
∴y1+y2+…+yn=18n,
则mx1+ky1,mx2+ky2,…,mxn+kyn的平均数=$\frac{m{x}_{1}+k{y}_{1}+m{x}_{2}+k{y}_{2}+…+m{x}_{n}+k{y}_{n}}{n}$
=$\frac{m({x}_{1}+{x}_{2}+…+{x}_{n})+k({y}_{1}+{y}_{2}+…+{y}_{n})}{n}$
=m×4+k×18
=4m+18k.
点评 本题主要考查算术平均数的算法,熟练掌握平均数的计算公式是解决此题的关键.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案(1)在一个变化过程中,允许出现多个变量和常量;
(2)变量就是变量,它不可以转化为常量;
(3)变量和常量是相对而言的,在一定条件下可以相互转化;
(4)在一个变化过程中,变量只有2个,常量可以没有,也可能有多个.
其中正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
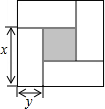 如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )| A. | x+y=7 | B. | x-y=2 | C. | x2-y2=4 | D. | 4xy+4=49 |
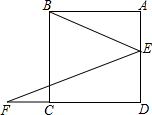 如图,点E为正方形ABCD的边AD上一点,F在DC的延长线上,且CF=AE.
如图,点E为正方形ABCD的边AD上一点,F在DC的延长线上,且CF=AE.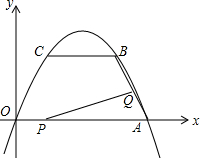 已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.
已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.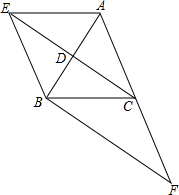 已知:如图,在△ABC中,CD是中线,过点A作BC的平行线交CD的延长线于点E,连接EB.
已知:如图,在△ABC中,CD是中线,过点A作BC的平行线交CD的延长线于点E,连接EB.