题目内容
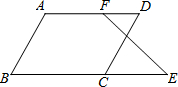
如图，已知△ACF≌△DBE，AD=9厘米，BC=5厘米，求AB的长．考点：全等三角形的性质
专题：
分析：AB不是全等三角形的对应边，但它通过全等三角形的对应边转化为AB=CD，而使AB+CD=AD-BC可利用已知的AD与BC求得．
解答：解：∵△ACF≌△DBE，
∴CA=BD，
∴CA-BC=DB-BC，
即AB=CD，
∴AB+CD=2AB=AD-BC=9-5=4（cm），
∴AB=2cm．
∴CA=BD，
∴CA-BC=DB-BC，
即AB=CD，
∴AB+CD=2AB=AD-BC=9-5=4（cm），
∴AB=2cm．
点评：本题主要考查了全等三角形的对应边相等．难点在于根据图形得到线段AB=CD，也是解决本题的关键．
练习册系列答案
相关题目
如果一个三角形的两条边长分别为2和6，那么这个三角形的周长可能是（ ）
| A、10 | B、11 |
| C、12 | D、14.2 |
在括号内填写理由．