题目内容
解不等式:5(x+2)≥1-2(x-1),并将解集在数轴上表示出来.
考点:解一元一次不等式,在数轴上表示不等式的解集
专题:
分析:根据不等式的性质,先去括号,然后移项、系数化为1,即可求得不等式的解集,然后在数轴上表示出解集.
解答:解:去括号得:5x+10≥1-2x+2,
移项得:5x+2x≥1+2-10,
合并同类项得:7x≥-7,
解得:x≥-1.
在数轴上表示为:
 .
.
移项得:5x+2x≥1+2-10,
合并同类项得:7x≥-7,
解得:x≥-1.
在数轴上表示为:
 .
.点评:本题考查了解一元一次不等式,解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

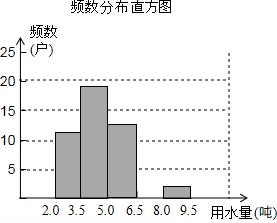 某市在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽取获得的50个家庭去年的月人均用水量(单位:吨)的调查数据进行研究了如下整理:
某市在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽取获得的50个家庭去年的月人均用水量(单位:吨)的调查数据进行研究了如下整理:
 在括号内填写理由.
在括号内填写理由.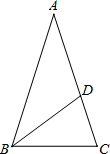 如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
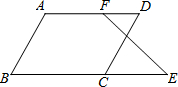
如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x. 如图,矩形ABCD中,AD=
如图,矩形ABCD中,AD=