题目内容
9.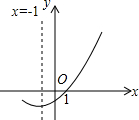 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1,x2的值分别是( )
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1,x2的值分别是( )| A. | -2,1 | B. | -3,1 | C. | -1,1 | D. | 不能确定 |
分析 根据二次函数y=ax2+bx+c图象的一部分可知该抛物线的对称轴是x=-1,然后由抛物线的对称性求得该图象与x轴的另一个交点,即方程ax2+bx+c=0的另一个解.
解答 解:根据图示知,抛物线y=ax2+bx+c图象的对称轴是x=-1,与x轴的一个交点坐标为(1,0),
根据抛物线的对称性知,抛物线y=ax2+bx+c图象与x轴的两个交点关于直线x=-1对称,即
抛物线y=ax2+bx+c图象与x轴的另一个交点与(1,0)关于直线x=-1对称,
∴另一个交点的坐标为(-3,0),
∴方程ax2+bx+c=0的另一个解是x=-3;
∴方程ax2+bx+c=0的两根分别为:1,-3.
故选B.
点评 本题考查了抛物线与x轴的交点.解该题时,充分利用了抛物线的对称性.

练习册系列答案
相关题目
19.若分式$\frac{|x|-3}{x-3}$=1,则x的值为( )
| A. | x≥0 | B. | x>3 | C. | x≥0且x≠3 | D. | x≠3 |
19.用加减消元法解方程组$\left\{\begin{array}{l}{4x+3y=2}\\{3x-4y=7}\end{array}\right.$时,有下列四种变形,其中正确的是( )
| A. | $\left\{\begin{array}{l}{12x+9y=2}\\{12x-16y=7}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{12x+3y=6}\\{12x-4y=28}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{12x+9y=6}\\{12x-16y=28}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{16x+12y=2}\\{9x-12y=7}\end{array}\right.$ |
 如图,在△ABC中,DE∥CB,若AD:DC=3:1,EB=2,则AE=6.
如图,在△ABC中,DE∥CB,若AD:DC=3:1,EB=2,则AE=6. 如图,在△ABC中,DE∥BC,EC=2AE,BD=6,则AD=3.
如图,在△ABC中,DE∥BC,EC=2AE,BD=6,则AD=3.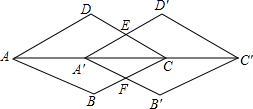 如图,将菱形ABCD沿AC方向平移至A′B′C′D′,A′D′交CD于点C,A′B′交BC于点F,判断A′FCE是不是菱形,并说明理由.
如图,将菱形ABCD沿AC方向平移至A′B′C′D′,A′D′交CD于点C,A′B′交BC于点F,判断A′FCE是不是菱形,并说明理由.