题目内容
19.若分式$\frac{|x|-3}{x-3}$=1,则x的值为( )| A. | x≥0 | B. | x>3 | C. | x≥0且x≠3 | D. | x≠3 |
分析 直接利用分式的性质结合绝对值的性质化简求出即可.
解答 解:∵分式$\frac{|x|-3}{x-3}$=1,
∴|x|-3=x-3,x-3≠0,
则|x|=x,
解得:x≥0且x≠3.
故选:C.
点评 此题主要考查了分式的值,正确利用分式的性质化简求出是解题关键.

练习册系列答案
相关题目
9.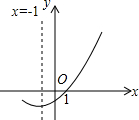 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1,x2的值分别是( )
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1,x2的值分别是( )
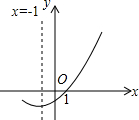 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1,x2的值分别是( )
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1,x2的值分别是( )| A. | -2,1 | B. | -3,1 | C. | -1,1 | D. | 不能确定 |
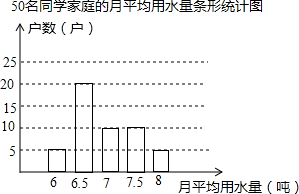 为了倡导“节约用水从我做起”,王伟同学在本校八年级的450名同学中,随机调查了50名同学家庭2012年1月至2012年10月的月平均用水量(单位:吨),并将调查结果绘成了下图所示的条形统计图.
为了倡导“节约用水从我做起”,王伟同学在本校八年级的450名同学中,随机调查了50名同学家庭2012年1月至2012年10月的月平均用水量(单位:吨),并将调查结果绘成了下图所示的条形统计图.