题目内容
18．
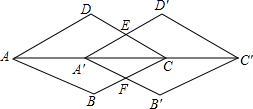如图，将菱形ABCD沿AC方向平移至A′B′C′D′，A′D′交CD于点C，A′B′交BC于点F，判断A′FCE是不是菱形，并说明理由．
分析 先证明四边形A′FCE是平行四边形，再证EA′=EC，即可得出结论．
解答 解：四边形A′FCE是菱形；理由如下：
∵四边形ABCD是菱形，
∴AD=CD，AD∥BC，AB∥CD，∠DAC=∠DCA，
∵菱形ABCD沿AC方向平移至A′B′C′D′，
∴AD∥A′D′，DC∥D′C′，
∴∠DAC=∠D′A′C，A′E∥BC，CE∥A′B′，
∴四边形A′FCE是平行四边形，∠D′A′C=∠DCA，
∴EA′=EC，
∴四边形A′FCE是菱形．
点评 本题考查了菱形的判定与性质、平移的性质，平行四边形的判定以及等腰三角形的判定；熟练掌握菱形的性质与判定是解决问题的关键．
练习册系列答案
口算能手系列答案
相关题目
9．
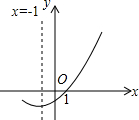如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，则关于x的一元二次方程ax2+bx+c=0（a≠0）的解x1，x2的值分别是（ ）
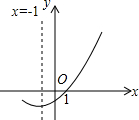如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，则关于x的一元二次方程ax2+bx+c=0（a≠0）的解x1，x2的值分别是（ ）| A． | -2，1 | B． | -3，1 | C． | -1，1 | D． | 不能确定 |
如图，△ABC中，如果AB=AC，AD⊥BC于点D，M为AC中点，AD与BM交于点G，那么S△GDM：S△GAB的值为1：4．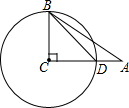
如图，在△ABC中，已知∠C=90°，sinA=$\frac{3}{5}$，以BC为半径的⊙C交AC边上一点D，若AD=4，求半径BC的长．
如图是两个互相啮合的齿轮，它们在同一时间内转动时，大齿轮和小齿轮转过的总齿数是相同的，尝试回答下面问题．