题目内容
19．用加减消元法解方程组$\left\{\begin{array}{l}{4x+3y=2}\\{3x-4y=7}\end{array}\right.$时，有下列四种变形，其中正确的是（ ）| A． | $\left\{\begin{array}{l}{12x+9y=2}\\{12x-16y=7}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{12x+3y=6}\\{12x-4y=28}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{12x+9y=6}\\{12x-16y=28}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{16x+12y=2}\\{9x-12y=7}\end{array}\right.$ |
分析 用加减消元法，消去x，第一个方程两边乘以3，第二个方程两边乘以4，变形得到结果，即可做出判断．
解答 解：用加减消元法解方程组时，变形为$\left\{\begin{array}{l}{12x+9y=6}\\{12x-16y=28}\end{array}\right.$，
故选C
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
9．
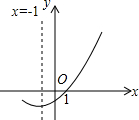如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，则关于x的一元二次方程ax2+bx+c=0（a≠0）的解x1，x2的值分别是（ ）
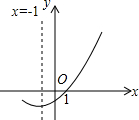如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，则关于x的一元二次方程ax2+bx+c=0（a≠0）的解x1，x2的值分别是（ ）| A． | -2，1 | B． | -3，1 | C． | -1，1 | D． | 不能确定 |
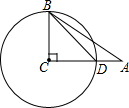如图，在△ABC中，已知∠C=90°，sinA=$\frac{3}{5}$，以BC为半径的⊙C交AC边上一点D，若AD=4，求半径BC的长．
如图是两个互相啮合的齿轮，它们在同一时间内转动时，大齿轮和小齿轮转过的总齿数是相同的，尝试回答下面问题．
如图，已知?ABCD中，P是∠B、∠C的平分线上的交点，PM⊥BC于M，若BP=4+$\sqrt{2}$，CP=4-$\sqrt{2}$，求PM的长．