题目内容

14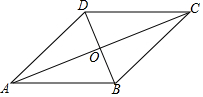．如图，在菱形ABCD中，对角线AC与BD相交于点O，若∠ADC=130°，则∠DAC的大小为（　　）
A．75°B．65°C．25°D．50°

分析 根据菱形的性质可得DC∥AB，∠DAC=$\frac{1}{2}$∠DAB，利用平行线的性质可得∠DAB=50°，进而可得答案．

解答 解：∵四边形ABCD是菱形，
∴DC∥AB，∠DAC=$\frac{1}{2}$∠DAB，
∵∠ADC=130°，
∴∠DAB=50°，
∴∠DAC=25°，
故选：C．

点评 此题主要考查了菱形的性质，关键是掌握菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．

练习册系列答案
相关题目

如图，已知点D在反比例函数y＝的图象上，过点D作x轴的平行线交y轴于点B（0,3）．过点A（5,0）的直线y＝kx＋b与y轴于点C，且BD＝OC，tan∠OAC＝．

(1)求反比例函数y＝和直线y＝kx＋b的解析式；

(2)连接CD，试判断线段AC与线段CD的关系，并说明理由；

(3)点E为x轴上点A右侧的一点，且AE＝OC，连接BE交直线CA与点M，求∠BMC的度数．
7．计算：$\frac{{1000}^{2}}{{625}^{2}{-375}^{2}}$=4．
2．已知n是一个正整数，$\sqrt{12n}$是整数，则n的最小值是（　　）
A．1B．2C．3D．4
9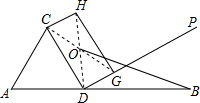．如图，线段AB的长为20，点D在AB上，△ACD是边长为8的等边三角形，过点D作与CD垂直的射线DP，过DP上一动点G（不与D重合）作矩形CDGH，记矩形CDGH的对角线交点为O，连接OB，则线段BO的最小值为（　　）
A．10B．6C．8$\sqrt{3}$D．6$\sqrt{3}$
19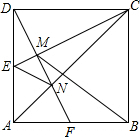．如图，在正方形ABCD中，E为AD的中点，DF⊥CE于M，交AC于点N，交AB于点F，连接EN、BM．有如下结论：①△ADF≌△DCE；②MN=FN；③△DMC∽△EMN；④BM=AB；其中正确结论的个数为（　　）
A．1个B．2个C．3个D．4个
6．甲乙两城市相距600千米，一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市，已知货车出发1小时后客车再出发，先到终点的车辆原地休息，在汽车行驶过程中，设两车之间的距离为s（千米），客车出发的时间为t（小时），它们之间的关系如图所示，则下列结论正确的有（　　）个
①货车的速度是60千米/小时；②离开出发地后，两车第一次相遇时，距离出发地150千米；③货车从出发地到终点共用时7小时；④客车到达终点时，两车相距180千米．
A．1B．2C．3D．4
2．如图，在数轴上点A表示的数的相反数可能是（　　）
A．1.5B．-1.5C．-2.4D．2.4
3．点P（-2，5）在坐标系中的位置在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网