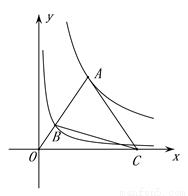题目内容
如图,已知点D在反比例函数y= 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= .
.
(1)求反比例函数y= 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.

练习册系列答案
相关题目
14.下列式子:①$\sqrt{{a^2}+{b^2}}$,②$\sqrt{\frac{x}{b}}$,③$\sqrt{{x^2}-xy}$,④$\sqrt{27ab}$中,是最简二次根式的是( )
| A. | ①④ | B. | ③④ | C. | ①③ | D. | ①② |
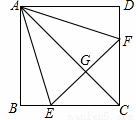
15. 如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
 如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )| A. | △AGC中,CF是AG边上的高 | B. | △GBC中,CF是BG边上的高 | ||
| C. | △ABC中,GC是BC边上的高 | D. | △GBC中,GC是BC边上的高 |
14.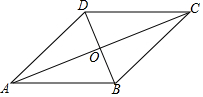 如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )| A. | 75° | B. | 65° | C. | 25° | D. | 50° |



 B.
B. C.
C. D.
D.
 的值与
的值与 的值相等,则
的值相等,则 的值为____.
的值为____. B.
B.  C.
C.  D.
D. 
 (x>0)图象上一点,连接OA,交函数y=
(x>0)图象上一点,连接OA,交函数y= (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为________________.
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为________________.