题目内容
7.计算:$\frac{{1000}^{2}}{{625}^{2}{-375}^{2}}$=4.分析 先依据平方差公式计算分母部分,然后再进行约分即可.
解答 解:原式=$\frac{100{0}^{2}}{(625+375)(625-375)}$=$\frac{100{0}^{2}}{1000×250}$=4.
故答案为:4.
点评 本题主要考查的是平方差公式的应用,熟练掌握平方差公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
 如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )
如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是( )| A. | △AGC中,CF是AG边上的高 | B. | △GBC中,CF是BG边上的高 | ||
| C. | △ABC中,GC是BC边上的高 | D. | △GBC中,GC是BC边上的高 |
2.(-$\frac{5}{13}$)2003×(-2$\frac{3}{5}$)2003=( )
| A. | -1 | B. | 1 | C. | 0 | D. | 2003 |
12.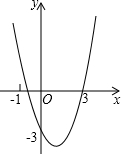 如图,抛物线过(-1,0),(3,0),(0,-3)三点,沿x轴方向平移抛物线,使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4,则符合条件的平移方式有( )
如图,抛物线过(-1,0),(3,0),(0,-3)三点,沿x轴方向平移抛物线,使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4,则符合条件的平移方式有( )
 如图,抛物线过(-1,0),(3,0),(0,-3)三点,沿x轴方向平移抛物线,使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4,则符合条件的平移方式有( )
如图,抛物线过(-1,0),(3,0),(0,-3)三点,沿x轴方向平移抛物线,使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4,则符合条件的平移方式有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.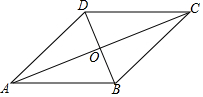 如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )| A. | 75° | B. | 65° | C. | 25° | D. | 50° |
14.Rt△ABC中,∠C=90°,∠B=40°,则∠A=( )
| A. | 60° | B. | 30° | C. | 50° | D. | 40° |

 B.
B. C.
C. D.
D.
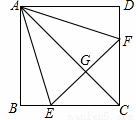
 ,则阴影部分的面积为( )
,则阴影部分的面积为( )
 C.
C.  D.
D. 