题目内容
6. 甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市,已知货车出发1小时后客车再出发,先到终点的车辆原地休息,在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论正确的有( )个
甲乙两城市相距600千米,一辆货车和一辆客车均从甲城市出发匀速行驶至乙城市,已知货车出发1小时后客车再出发,先到终点的车辆原地休息,在汽车行驶过程中,设两车之间的距离为s(千米),客车出发的时间为t(小时),它们之间的关系如图所示,则下列结论正确的有( )个①货车的速度是60千米/小时;②离开出发地后,两车第一次相遇时,距离出发地150千米;③货车从出发地到终点共用时7小时;④客车到达终点时,两车相距180千米.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 通过函数图象可得,货车出发1小时走的路程为60千米,客车到达终点所用的时间为6小时,根据行程问题的数量关系可以求出货车和客车的速度,利用数形结合思想及一元一次方程即可解答.
解答 解:由函数图象,得:货车的速度为60÷1=60千米/小时,客车的速度为600÷6=100千米/小时,故①正确;
设客车离开起点x小时后,甲、乙两人第一次相遇,根据题意得:
100x=60+60x,
解得:x=1.5,
∴离开起点后,两车第一次相遇时,距离起点为:1.5×100=150(千米),
故②正确;
甲从起点到终点共用时为:600÷60=10(小时),
故③错误;
∵客车到达终点时,所用时间为6小时,货车先出发1小时,
∴此时货车行走的时间为7小时,
∴货车走的路程为:7×60=420(千米),
∴客车到达终点时,两车相距:600-420=180(千米),故④正确.
故选:C.
点评 本题主要考查了函数图象的读图能力,要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.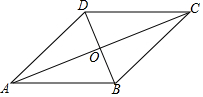 如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )| A. | 75° | B. | 65° | C. | 25° | D. | 50° |
1.圆锥的主视图是边长为4cm的等边三角形,则该圆锥俯视图的面积是( )
| A. | 4π cm2 | B. | 8π cm2 | C. | 12π cm2 | D. | 16π cm2 |
18.已知关于x的一元二次方程x2-2x+k=0有两个不相等的实数根,则k的值可以是( )
| A. | -2 | B. | 1 | C. | 2 | D. | 3 |
14.Rt△ABC中,∠C=90°,∠B=40°,则∠A=( )
| A. | 60° | B. | 30° | C. | 50° | D. | 40° |
15.方程x2=9的解是( )
| A. | 3 | B. | ±3 | C. | 81 | D. | ±81 |
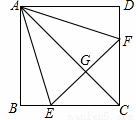
 ,则阴影部分的面积为( )
,则阴影部分的面积为( )
 C.
C.  D.
D. 
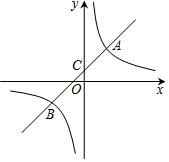 如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,6)与点B,且与y轴交于点C,若点P是反比例函数y=$\frac{k}{x}$图象上的一个动点,作直线AP与x轴、y轴分别交于点M、N,连结BN、CM.若S△ACM=S△ABN,则$\frac{AP}{AN}$的值为2或4.
如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,6)与点B,且与y轴交于点C,若点P是反比例函数y=$\frac{k}{x}$图象上的一个动点,作直线AP与x轴、y轴分别交于点M、N,连结BN、CM.若S△ACM=S△ABN,则$\frac{AP}{AN}$的值为2或4.