题目内容
2．已知n是一个正整数，$\sqrt{12n}$是整数，则n的最小值是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 先化简二次根式，然后依据化简结果为整数可确定出n的值．
解答 解：$\sqrt{12n}$=2$\sqrt{3n}$．
∵n是一个正整数，$\sqrt{12n}$是整数，
∴n的最小值是3．
故选：C．
点评 本题主要考查的是二次根式的定义，熟练掌握二次根式的定义是解题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
的值与
的值相等，则
的值为____．
15．
如图，AD⊥BC于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中错误的是（ ）
如图，AD⊥BC于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中错误的是（ ）| A． | △AGC中，CF是AG边上的高 | B． | △GBC中，CF是BG边上的高 | ||
| C． | △ABC中，GC是BC边上的高 | D． | △GBC中，GC是BC边上的高 |
12．
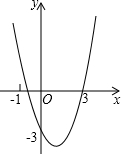如图，抛物线过（-1，0），（3，0），（0，-3）三点，沿x轴方向平移抛物线，使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4，则符合条件的平移方式有（ ）
如图，抛物线过（-1，0），（3，0），（0，-3）三点，沿x轴方向平移抛物线，使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4，则符合条件的平移方式有（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
，则阴影部分的面积为( )
C. 
D. 
7．若顺次连接四边形ABCD四边的中点，得到一个四边形，则此四边形一定是（ ）
| A． | 平行四边形 | B． | 矩形 | C． | 菱形 | D． | 正方形 |
14．
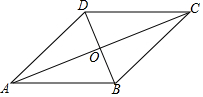如图，在菱形ABCD中，对角线AC与BD相交于点O，若∠ADC=130°，则∠DAC的大小为（ ）
如图，在菱形ABCD中，对角线AC与BD相交于点O，若∠ADC=130°，则∠DAC的大小为（ ）| A． | 75° | B． | 65° | C． | 25° | D． | 50° |
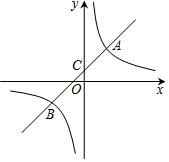如图，一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A（3，6）与点B，且与y轴交于点C，若点P是反比例函数y=$\frac{k}{x}$图象上的一个动点，作直线AP与x轴、y轴分别交于点M、N，连结BN、CM．若S△ACM=S△ABN，则$\frac{AP}{AN}$的值为2或4．
11．若-$\frac{3}{2}$x2y2m-1是五次单项式，那么m的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |