题目内容
9.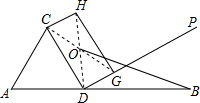 如图,线段AB的长为20,点D在AB上,△ACD是边长为8的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )
如图,线段AB的长为20,点D在AB上,△ACD是边长为8的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )| A. | 10 | B. | 6 | C. | 8$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
分析 连接AO,根据矩形对角线相等且互相平分得:OC=OD,再证明△ACO≌△ADO,则∠OAB=30°;点O一定在∠CAB的平分线上运动,根据垂线段最短得:当OB⊥AO时,OB的长最小,根据直角三角形30度角所对的直角边是斜边的一半得出结论.
解答  解:连接AO,
解:连接AO,
∵四边形CDGH是矩形,
∴CG=DH,OC=$\frac{1}{2}$CG,OD=$\frac{1}{2}$DH,
∴OC=OD,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
在△ACO和△ADO中$\left\{\begin{array}{l}{AC=AC}\\{AO=AO}\\{CO=DO}\end{array}\right.$,
∴△ACO≌△ADO(SSS),
∴∠OAB=∠CAO=$\frac{1}{2}$×60°=30°,
∴点O一定在∠CAB的平分线上运动,所以当OB⊥AO时,OB的长最小,
∵∠OAB=30°,∠AOB=90°,
∴OB=$\frac{1}{2}$AB=$\frac{1}{2}$×20=10(cm),
即OB的最小值为10cm,
故选:A.
点评 本题考查了矩形的性质、全等三角形的性质和判定、含30°角的直角三角形的性质,熟练掌握直角三角形中,30°角所对的直角边等于斜边的一半,利用了矩形对角线相等且平分的性质得对角线的一半相等,为三角形全等用铺垫;另外还利用了垂线段最短解决了求最值问题.

练习册系列答案
相关题目
2.(-$\frac{5}{13}$)2003×(-2$\frac{3}{5}$)2003=( )
| A. | -1 | B. | 1 | C. | 0 | D. | 2003 |
4.与2和为0的数是( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
14.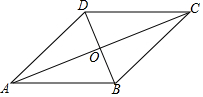 如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )| A. | 75° | B. | 65° | C. | 25° | D. | 50° |
1.圆锥的主视图是边长为4cm的等边三角形,则该圆锥俯视图的面积是( )
| A. | 4π cm2 | B. | 8π cm2 | C. | 12π cm2 | D. | 16π cm2 |
18.已知关于x的一元二次方程x2-2x+k=0有两个不相等的实数根,则k的值可以是( )
| A. | -2 | B. | 1 | C. | 2 | D. | 3 |
18.已知点(1,y1),(2,y2)是抛物线y=x2-6x上的两点,则y1,y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
 B.
B.  C.
C.  D.
D. 
 ,则阴影部分的面积为( )
,则阴影部分的面积为( )
 C.
C.  D.
D. 