Question

6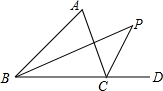．如图，在△ABC中，∠ABC的平分线BP与∠ACD的平分线CP交于P点．
（1）若∠ABC=50°，∠ACB=70°，求∠P的度数；
（2）若∠A=80°，则∠P的度数为40°；
（3）∠A与∠P之间存在怎样的数量关系，并加以说明．

Answer 1

分析 （1）根据三角形的内角和求得∠A，由BP是∠ABC的平分线，CP是∠ACD的平分线，可得∠PBC=$\frac{1}{2}$∠ABC，∠PCD=$\frac{1}{2}$∠ACD，然后由三角形外角的性质求得∠P=$\frac{1}{2}$∠A；
（2）BP是∠ABC的平分线，CP是∠ACD的平分线，可得∠PBC=$\frac{1}{2}$∠ABC，∠PCD=$\frac{1}{2}$∠ACD，然后由三角形外角的性质求得∠P=$\frac{1}{2}$∠A；
（3）运用三角形的一个外角等于和它不相邻的两个内角和以及角平分线的概念，推导得出∠P和∠A之间的关系．

解答 解：（1）∵∠A+∠ABC+∠ACB=180°，且∠ABC=50°，∠ACB=70°，
∴∠A=60°．
∵∠ACD是△ABC的外角，
∴∠ACD=∠A+∠ABC=110°．
∵∠ABC、∠ACD的平分线交于点P，
∴∠PBC=25°，∠PCD=55°，
∵∠PCD是△PBC的外角，
∴∠P=∠PCD-∠PBC=30°；

（2）∵∠PCD是△PBC的外角，
∴∠P=∠PCD-∠PBC．
∵∠ABC、∠ACD的平分线交于点P，
∴∠PBC=$\frac{1}{2}$∠ABC，∠PCD=$\frac{1}{2}$∠ACD．
∵∠ACD是△ABC的外角，
∴∠ACD=∠A+∠ABC，
∴∠P=$\frac{1}{2}$（∠A+∠ABC）-$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠A=40°；
故答案为：40°．

（3）∠P=$\frac{1}{2}$∠A．
∵∠ABC的平分线与△ABC的外角∠ACD的平分线交于点P，
∴∠ABP=∠CBP（设为α），∠PCD=$\frac{1}{2}$∠ACD；
∵∠ACD=∠A+∠ABC=∠A+2α，
∴∠PCD=$\frac{1}{2}$∠A+α；
又∵∠PCD=∠P+α，
∴∠P=$\frac{1}{2}$∠A．

点评 此题主要考查了三角形的内角和定理，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°．此题还考查了三角形的外角的性质和应用，要熟练掌握，解答此题的关键是要明确：①三角形的外角和为360°．②三角形的一个外角等于和它不相邻的两个内角的和．③三角形的一个外角大于和它不相邻的任何一个内角．