题目内容
12.汶川县组织20辆汽车装运完A、B、C三种土特产共100吨到外地销售,按计划,20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题.| 土特产品种 | A | B | C |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨土特产获利(百元) | 12 | 16 | 10 |
| 装运土特产的品种 | A | B | C |
| 汽车车辆(数) | x | y | |
| 装运的土特产数量(吨) | 6x | 5y |
分析 (1)根据装运A、B、C三种特产车共20辆,可表示出C种车辆数,再由每辆汽车需装载4吨特产可得装运的数量,由装运三种特产共100吨可列方程,进而表示出函数关系式;
(2)根据装运每种土特产的车辆都不少于5辆求出x的取值范围,由总利润等于A、B、C三种利润之和列出函数关系式,结合自变量取值范围求得最值情况.
解答 解:(1)根据题意,装运A种土特产的车辆数为x,装运B种土特产的车辆数为y,
那么装运C种土特产的车辆数为20-x-y,装载土特产的数量为4(20-x-y),
则有:6x+5y+4(20-x-y)=100
整理得:y=-2x+20;
完成表格如下:
| 装运土特产的品种 | A | B | C |
| 汽车车辆(数) | x | y | 20-x-y |
| 装运的土特产数量(吨) | 6x | 5y | 4(20-x-y) |
由题意得:$\left\{\begin{array}{l}{x≥5}\\{-2x+20≥5}\end{array}\right.$
解得:5≤x≤7.5,
设利润为W(百元)则:W=6x•12+5(-2x+20)•16+4x•10=-48x+1600,
∵k=-48<0,
∴W的值随x的增大而减小,
要使利润W最大,则x=5,W最大=-48×5+1600=1360(百元)=13.6(万元)
答:当装运A种土特产5车,B种土特产10车,C种土特产5车时,获利最大,最大利润为13.6万元.
点评 本题主要考查一次函数的实际应用能力,关键在复杂的数量关系中理清并找到所需的数量,确定等量关系是列方程和函数解析式的关键所在.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知∠A=45°,则∠A的补角等于( )
| A. | 45° | B. | 90° | C. | 135° | D. | 180° |
2.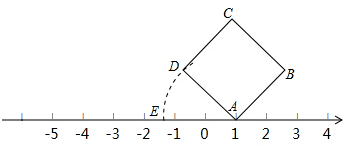 如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
 如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )| A. | $-\sqrt{5}$ | B. | $1-\sqrt{5}$ | C. | $\frac{{-1-\sqrt{5}}}{2}$ | D. | $\frac{3}{2}-\sqrt{5}$ |
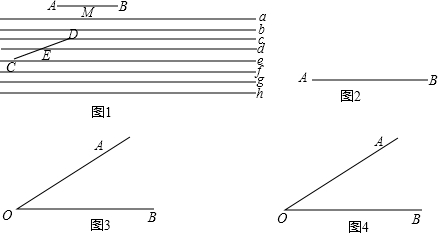
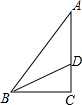 在直角三角形ABC中,BC=6cm,AC=8cm,点D在线段AC上从C向A运动.若设CD=x(m),△ABD的面积为因变量y.
在直角三角形ABC中,BC=6cm,AC=8cm,点D在线段AC上从C向A运动.若设CD=x(m),△ABD的面积为因变量y. 如图,∠AOC是直角,OC为∠BOD的平分线,且∠AOB=55°,求∠AOD的度数.
如图,∠AOC是直角,OC为∠BOD的平分线,且∠AOB=55°,求∠AOD的度数.