题目内容
4.从-1,0,1,3,4,这五个数中任选一个数记为a,则使双曲线y=$\frac{7-3a}{x}$在第一、三象限且不等式组$\left\{\begin{array}{l}{2x+3>9}\\{x-a<0}\end{array}\right.$无解的概率是$\frac{3}{5}$.分析 由双曲线y=$\frac{7-3a}{x}$在第一、三象限且不等式组$\left\{\begin{array}{l}{2x+3>9}\\{x-a<0}\end{array}\right.$无解,可求得a的取值范围,然后直接利用概率公式求解即可求得答案.
解答 解:∵双曲线y=$\frac{7-3a}{x}$在第一、三象限,
∴7-3a>0,
解得:a<$\frac{7}{3}$,
∵不等式组$\left\{\begin{array}{l}{2x+3>9}\\{x-a<0}\end{array}\right.$无解,
∴a≤3,
∴双曲线y=$\frac{7-3a}{x}$在第一、三象限且不等式组$\left\{\begin{array}{l}{2x+3>9}\\{x-a<0}\end{array}\right.$无解,则a<$\frac{7}{3}$,
即a=-1,0,1;
∴使双曲线y=$\frac{7-3a}{x}$在第一、三象限且不等式组$\left\{\begin{array}{l}{2x+3>9}\\{x-a<0}\end{array}\right.$无解的概率是:$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 此题考查了概率公式的应用以及反比例函数的性质、不等式组无解.注意根据题意求得a的取值范围是关键.

练习册系列答案
相关题目
15.为了测试某种汽车在高速路上匀速行驶的耗油量,专业测试员将汽车加满油,对汽车行驶中的情况做了记录,并把试验的数据制成如下表所示:
(1)根据上表的数据,请用x表示y,y=60-8x.
(2)若油箱中的剩余油量为20升,汽车行驶了多少小时?
(3)若该汽车贮满汽油准备从高速路出发,要匀速前往需要7小时车程的某目的地,当余油量不足5升时,油箱将会报警,请问汽车能在油箱报警之前到达目的地吗?请说明理由.
| 汽车行驶时间x(h) | 0 | 1 | 2 | 3 | … |
| 剩余油量y(L) | 60 | 52 | 44 | 36 | … |
(2)若油箱中的剩余油量为20升,汽车行驶了多少小时?
(3)若该汽车贮满汽油准备从高速路出发,要匀速前往需要7小时车程的某目的地,当余油量不足5升时,油箱将会报警,请问汽车能在油箱报警之前到达目的地吗?请说明理由.
12.汶川县组织20辆汽车装运完A、B、C三种土特产共100吨到外地销售,按计划,20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题.
(1)设装运A种土特产的车辆数为x辆,装运B种土特产的车辆数为y辆,填写下列表格,并求出y与x之间的函数关系式.
(2)如果装运每种土特产的车辆都不少于5辆,请设计出一种装运方案,使此次销售获利最大,并求出最大利润的值.
| 土特产品种 | A | B | C |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨土特产获利(百元) | 12 | 16 | 10 |
| 装运土特产的品种 | A | B | C |
| 汽车车辆(数) | x | y | |
| 装运的土特产数量(吨) | 6x | 5y |
19.若单项式m3xny+5与4m2-4yn2x是同类项,则下列哪项正确( )
| A. | x=1,y=2 | B. | x=2,y=-1 | C. | x=0,y=2 | D. | x=3,y=1 |
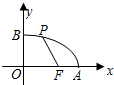 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③.
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③. 如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.
如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上. 如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$.
如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$.