Question

13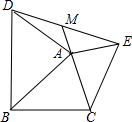．在△ABC中，AB≠AC，分别以AB，AC为边作等腰△ABD和△ACE，AD=AB，AC=AE，且∠ACB=∠BAD=∠CAE=α，连接DE，交CA延长线于点M，求证：M为DE中点．

Answer 1

分析 延长AM到F使AF=BC，连接DF，过E作EG∥DF交CM于G，根据三角形的内角和和平角的定义得到∠ABC=∠DAF=180°-∠BAC，推出△ADF≌△ABC，根据全等三角形的性质得到DF=AC，∠F=∠ACB=α，根据平行线的性质得到∠AGE=∠F=α，于是得到∠CAE=∠AGE，求得AE=EG，等量代换得到DF=EG，证得△DFM≌△GEM，根据全等三角形的性质即可得到结论．

解答 证明：延长AM到F使AF=BC，连接DF，过E作EG∥DF交CM于G，
∵∠DAB=∠ACB=α，
∵∠ABC=∠DAF=180°-∠BAC，
在△ADF与△ABC中，
$\left\{\begin{array}{l}{AD=AB}\\{∠DAF=∠ABC}\\{AF=BC}\end{array}\right.$，
∴△ADF≌△ABC，
∴DF=AC，∠F=∠ACB=α，
∵EG∥DF，
∴∠AGE=∠F=α，
∴∠CAE=∠AGE，
∴AE=EG，
∴DF=EG，
在△DFM与△EMG中，
$\left\{\begin{array}{l}{∠F=∠AGE}\\{∠DMF=∠GME}\\{DF=EG}\end{array}\right.$，
∴△DFM≌△GEM，
∴DM=EM，
∴M为DE中点．

点评 本题考查了全等三角形的判定和性质，等腰三角形的判定和性质，正确的作出辅助线是解题的关键．