题目内容
3.若a+b=3,ab=1,求(a4-b4)÷$\frac{{a}^{2}+{b}^{2}}{ab}$÷(a-b)的值.分析 先把除法改为乘法,约分化简后,进一步整体代入求得数值即可.
解答 解:(a4-b4)÷$\frac{{a}^{2}+{b}^{2}}{ab}$÷(a-b)
=(a2+b2)(a+b)(a-b)•$\frac{ab}{{a}^{2}+{b}^{2}}$•$\frac{1}{a-b}$
=ab(a+b),
当a+b=3,ab=1时,原式=3.
点评 此题考查分式的化简求值,掌握分式的化简方法与整体代入的方法是解决问题的关键.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
12.多项式的乘法法则知:若(x+a)(x+b)=x2+px+q,则p=a+b,q=a•b;反过来x2+px+q=(x+a)(x+b),要将多项式x2+px+q进行分解,关键是找到两个数a、b,使a+b=p,a•b=q,如对多项式x2-3x+2,有p=-3,q=2,a=-1,b=-2,此时(-1)+(-2)=-3,(-1)(-2)=2,所以x2-3x+2可分解为(x-1)(x-2),即x2-3x+2=(x-1)(x-2)
(1)根据以上填写下表:
(2)根据填表,还可得出如下结论:当q是正数时,应分解成两个因数a、b同号,a、b的符号与p相同;当q为负数时,应分解成的两个因数a、b异号,a、b中绝对值较大的因数的符合与p相同.
(3)分解因式x2-x-12=(x-4)(x+3);x2-7x+6=(x-1)(x-6).
(1)根据以上填写下表:
| 多项式 | p | q | a | b | 分解结果 |
| x2+9x+20 | 9 | 20 | 4 | 5 | (x+4)(x+5) |
| x2-9x+20 | -9 | 20 | -4 | -5 | (x-4)(x-5) |
(3)分解因式x2-x-12=(x-4)(x+3);x2-7x+6=(x-1)(x-6).
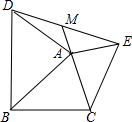 在△ABC中,AB≠AC,分别以AB,AC为边作等腰△ABD和△ACE,AD=AB,AC=AE,且∠ACB=∠BAD=∠CAE=α,连接DE,交CA延长线于点M,求证:M为DE中点.
在△ABC中,AB≠AC,分别以AB,AC为边作等腰△ABD和△ACE,AD=AB,AC=AE,且∠ACB=∠BAD=∠CAE=α,连接DE,交CA延长线于点M,求证:M为DE中点.