题目内容
1.已知:a=$\frac{1}{\sqrt{2}+1}$,化简并求$\frac{{a}^{2}+a-2}{a+2}$-$\frac{\sqrt{{a}^{2}-2a+1}}{{a}^{2}-a}$的值.分析 先化简a,再化简所求的代数式,代入a的值进行计算即可.
解答 解:a=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1,
原式=$\frac{(a-1)(a+2)}{a+2}$-$\frac{\sqrt{(a-1)^{2}}}{a(a-1)}$
=a-1+$\frac{1}{a}$,
原式=$\sqrt{2}$-1-1+$\sqrt{2}$+1
=2$\sqrt{2}$-1.
点评 本题考查了二次根式的化简求值,掌握二次根式的化简是解题的关键.

练习册系列答案
相关题目
9.如果P(-2,a)和Q(-3,b)都在正比例函数y=kx(k<0)的图象上,那么a和b的大小是( )
| A. | a>b | B. | a=b | C. | a<b | D. | 以上都有可能 |
10.下列运算正确的是( )
| A. | x4•x3=x12 | B. | (x3)2=x9 | C. | x4÷x3=x | D. | x3+x4=x7 |
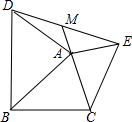 在△ABC中,AB≠AC,分别以AB,AC为边作等腰△ABD和△ACE,AD=AB,AC=AE,且∠ACB=∠BAD=∠CAE=α,连接DE,交CA延长线于点M,求证:M为DE中点.
在△ABC中,AB≠AC,分别以AB,AC为边作等腰△ABD和△ACE,AD=AB,AC=AE,且∠ACB=∠BAD=∠CAE=α,连接DE,交CA延长线于点M,求证:M为DE中点.