题目内容
9. 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,给出下列判断:
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,给出下列判断:①AM=BM;②AP=BN;③∠MAP=∠MBP;④AN∥BP.其中结论正确的是:①③(填上序号即可)
分析 根据直线MN是四边形AMBN的对称轴,得到点A与点B对称,根据轴对称的性质即可得到结论.
解答  解:∵直线MN是四边形AMBN的对称轴,
解:∵直线MN是四边形AMBN的对称轴,
∴点A与点B对应,
∴AM=BM,∠ANM=∠BNM,AN=BN,
∵点P是直线MN上的点,
∴∠MAP=∠MBP,AP=BP,
∴①③正确,②④错误,
故答案为:①③.
点评 本题考查了轴对称的性质,熟练掌握轴对称的性质是解题的关键.如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19.若二次函数y=x2+mx的对称轴是x=3,则抛物线y=x2+mx与x轴的交点坐标为( )
| A. | (0,0) | B. | (0,6) | C. | (0,0)和(0,6) | D. | (0,0)和(6,0) |
18.依次连接菱形的各边中点,得到的四边形是( )
| A. | 矩形 | B. | 平行四边形 | C. | 菱形 | D. | 梯形 |

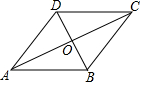 如图,?ABCD中,对角线AC,BD相交于点O,且AC⊥BD,请你添加一个适当的条件∠BAD=90°,使ABCD成为正方形.
如图,?ABCD中,对角线AC,BD相交于点O,且AC⊥BD,请你添加一个适当的条件∠BAD=90°,使ABCD成为正方形.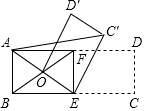 如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.
如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.