题目内容
19.若二次函数y=x2+mx的对称轴是x=3,则抛物线y=x2+mx与x轴的交点坐标为( )| A. | (0,0) | B. | (0,6) | C. | (0,0)和(0,6) | D. | (0,0)和(6,0) |
分析 由对称轴为x=3,可求出m的值,进而得到抛物线的解析式,再令y=0,解方程即可求出抛物线y=x2+mx与x轴的交点坐标.
解答 解:
∵二次函数y=x2+mx的对称轴是x=3,
∴x=-$\frac{m}{2}$=3,
∴m=-6,
∴y=x2-6x,
令y=0,则x2-6x=0,
解得:x=0或6,
∴抛物线y=x2+mx与x轴的交点坐标为(0,0)和(6,0),
故选D.
点评 本题考查了抛物线和x轴交点的问题,根据抛物线对称轴方程求出m的值是解题关键.

练习册系列答案
相关题目
14. 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )| A. | 两点之间的线段最短 | B. | 三角形具有稳定性 | ||
| C. | 长方形是轴对称图形 | D. | 长方形的四个角都是直角 |
8.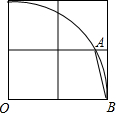 如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为( )
如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为( )
 如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为( )
如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为( )| A. | $2-\sqrt{3}$ | B. | 2 | C. | $2+\sqrt{3}$ | D. | 3 |

 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,给出下列判断:
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,给出下列判断: