Question

4．已知：在Rt△ABC中，∠C=90°，AB=5，BC=4，G是重心，GH⊥AB于H，求GH的长．

Answer 1

分析 根据勾股定理求出AC，根据三角形的面积公式求出△ABC的面积，根据中线的性质求出△ADB的面积，根据重心的性质得到AG=2GD，根据三角形的面积公式计算即可．

解答 解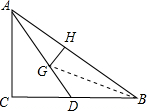：连接GB，
∵∠C=90°，AB=5，BC=4，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=3，
∴△ABC的面积为：$\frac{1}{2}$×3×4=6，
∵AD为△ABC的中线，
∴△ADB的面积为3，
∵G是重心，
∴AG=2GD，
∴△AGB的面积为2，
∴$\frac{1}{2}$×AB×GH=2，即$\frac{1}{2}$×5×GH=2，
解得，GH=0.8．

点评 本题考查的是三角形的重心的概念和性质：三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．