题目内容
14.在等腰梯形ABCD中,AD∥BC,延长DC到E,使得CE=CD,连接AE交BC于F,下面有三个结论:①AF=FE,②BF-FC=BC-CD,③AE>BC,其中正确的个数有2个.分析 ①根据平行线分线段成比例定理直接得出;
②作腰的平行线,证明△AGF≌△ECF,得FG=FC,则BF-FC=BC-CG,而且CG和CD不一定相等,所以结论不正确;
③作辅助线,构建?ABCM,证明△AEM是直角三角形,根据垂线段最短得AE>AM,则AE>BC,结论正确.
解答 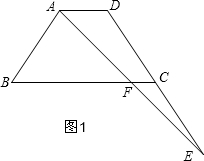 解:①如图1,∵AD∥BC,
解:①如图1,∵AD∥BC,
∴$\frac{EC}{DC}=\frac{EF}{AF}$,
∵DC=EC,
∴AF=FE;
所以此选项正确;
②如图2,过A作AG∥CD,交BC于G,
∴∠AGF=∠FCE,
∵AF=EF,∠AFG=∠EFC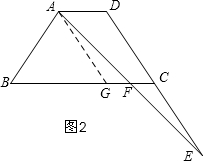 ,
,
∴△AGF≌△ECF,
∴FG=FC,
∴BF-FC=BF-FG=BG,
∵BG=BC-CG,
∴BF-FC=BC-CG,
只有当CG=CD时,BF-FC=BC-CD成立,
∵CG与CD不一定相等,
所以此选项不正确;
③如图3,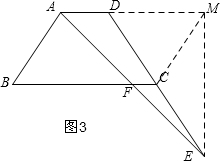 延长AD至M,使AM=BC,连接CM、EM,
延长AD至M,使AM=BC,连接CM、EM,
∵AM∥BC,
∴四边形ABCM是平行四边形,
∴CM=AB,
∴DC=CM=CE,
∴∠CDM=∠CMD,∠CME=∠CEM,
∴∠CDM+∠CEM=∠CMD+∠CME=90°,
∴△AEM是直角三角形,
∴AE>AM,
∴AE>BC,
所以此选项正确,
故本题正确的结论有2个,
故答案为:2.
点评 本题考查了直角梯形的性质和全等三角形的性质与判定,在梯形的问题中,常常需要辅助线的帮助解决问题,一般辅助线的作法是:①作高,②作对角线的平行线,③作腰的平行线等,通过辅助线构建平行四边形或全等三角形;本题的第③问有难度,比较两线段的大小,一般情况下,可以利用第三边转化,或利用辅助线将要比较大小的边放在同一三角形中来解决,本题就是利用了后一种方法.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
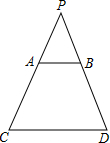 如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则点P到AB间的距离是0.9m.
如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则点P到AB间的距离是0.9m. 学校准备在围墙边设计一个长方形的自行车车棚,一边利用围墙,墙长为18米,并且已有总长为32m的铁围栏,为了出入方便,在平行于墙的一边留有一个2米宽的门(门另用其他材料做好)设与墙垂直的一边长为x米.
学校准备在围墙边设计一个长方形的自行车车棚,一边利用围墙,墙长为18米,并且已有总长为32m的铁围栏,为了出入方便,在平行于墙的一边留有一个2米宽的门(门另用其他材料做好)设与墙垂直的一边长为x米. 如图.已知DE∥AC,DF∥AB,BD:DC=2:5.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BD}$=$\overrightarrow{b}$.用$\overrightarrow{a}$、$\overrightarrow{b}$表示;
如图.已知DE∥AC,DF∥AB,BD:DC=2:5.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BD}$=$\overrightarrow{b}$.用$\overrightarrow{a}$、$\overrightarrow{b}$表示; 如图,Rt△ABC的顶点A是y=-x-m+3与y=-$\frac{m}{x}$的在第二象限的交点,且S△AOB=1,求A点的坐标.
如图,Rt△ABC的顶点A是y=-x-m+3与y=-$\frac{m}{x}$的在第二象限的交点,且S△AOB=1,求A点的坐标.