题目内容
如图,在平面直角坐标系中,直线y=x+6与x轴、y轴分别交于点A、B,直线CD:y =-
=-
x+m与直线AB交于点E,E点的横坐标为-
.
(1)求m的值;
(2)点P(t,0)在x轴上,作线段PD的垂直平分线交直线DE于M,交x轴与点F,过点M作x轴的平行线交直线AB于点N,设线段MN的长为d,当-6<t<8时,求d与t的函数关系式;
(3)在(2)的条件下,连接BP与BM,求当t为何值时∠PBM=45°,并直接写出此时点F的坐标.
 =-
=-| 1 |
| 2 |
| 4 |
| 3 |
(1)求m的值;
(2)点P(t,0)在x轴上,作线段PD的垂直平分线交直线DE于M,交x轴与点F,过点M作x轴的平行线交直线AB于点N,设线段MN的长为d,当-6<t<8时,求d与t的函数关系式;
(3)在(2)的条件下,连接BP与BM,求当t为何值时∠PBM=45°,并直接写出此时点F的坐标.
考点:一次函数综合题
专题:
分析:(1)根据一次函数图象上点的坐标特征,将点E的横坐标代入直线y=x+6中求得点E的纵坐标;然后将点E的坐标代入直线CD的解析式即可求得m的值;
(2)根据P点的坐标表示出点F的坐标,然后根据MN∥x轴表示出点M、N的坐标,从而求得函数的解析式;
(3)过点P作PG垂直于AB于点G,利用构建相似三角形△BPG∽△BMH,由相似三角形的对应边成比例来求t的值.
(2)根据P点的坐标表示出点F的坐标,然后根据MN∥x轴表示出点M、N的坐标,从而求得函数的解析式;
(3)过点P作PG垂直于AB于点G,利用构建相似三角形△BPG∽△BMH,由相似三角形的对应边成比例来求t的值.
解答:解:(1)∵点E在直线y=x+6上,且E点的横坐标为-
,
∴y=-
+6=
,即E(-
,
).
又∵点E也在直线y=-
x+m上,
∴
=-
×(-
)+m,
解得m=4,即m的值为4;
(2)由直线CD:y=-
x+4知,D(8,0).
∵点P(t,0),点F是线段PD的中点,
∴F(
,0).
又∵MF⊥PD,点M在直线CD上,
∴点M的横坐标与点F的横坐标都是
,则yM=-
•
+4=-
.
∵MN∥x轴,且点N在直线y=x+6上,
∴yN=yM=-
=xN+6,
解得xN=-
+6,
∴MN=xM-xN=
-6+
=
t-2,即d=
t-2(-6<t<8);
(3)如图,连接BP、BM.P作PG垂直于AB于点G.设MN交y轴于点H.
∵y=x+6与x轴、y轴分别交于点A、B,
∴A(-6,0),B(0,6),
∴OA=OB,
∴∠BAO=∠ABO=45°,
∴AG=PG=
(t+6).
∵∠PBM=45°,
∴∠GBP=∠FBM.
又∵∠BGP=∠BHM=90°,
∴△BPG∽△BMH,
∴
=
,即
=
,
解得t=0.
则点P与原点O重合,
∴OF=
OD=4,
∴F(4,0).
| 4 |
| 3 |
∴y=-
| 4 |
| 3 |
| 14 |
| 3 |
| 4 |
| 3 |
| 14 |
| 3 |
又∵点E也在直线y=-
| 1 |
| 2 |
∴
| 14 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
解得m=4,即m的值为4;
(2)由直线CD:y=-
| 1 |
| 2 |
∵点P(t,0),点F是线段PD的中点,
∴F(
| 8+t |
| 2 |
又∵MF⊥PD,点M在直线CD上,
∴点M的横坐标与点F的横坐标都是
| 8+t |
| 2 |
| 1 |
| 2 |
| 8+t |
| 2 |
| t |
| 4 |
∵MN∥x轴,且点N在直线y=x+6上,
∴yN=yM=-
| t |
| 4 |
解得xN=-
| t |
| 4 |

∴MN=xM-xN=
| 8+t |
| 2 |
| t |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
(3)如图,连接BP、BM.P作PG垂直于AB于点G.设MN交y轴于点H.
∵y=x+6与x轴、y轴分别交于点A、B,
∴A(-6,0),B(0,6),
∴OA=OB,
∴∠BAO=∠ABO=45°,
∴AG=PG=
| ||
| 2 |
∵∠PBM=45°,
∴∠GBP=∠FBM.
又∵∠BGP=∠BHM=90°,
∴△BPG∽△BMH,
∴
| BG |
| BH |
| PG |
| MH |
6
| ||||||
6-
|
| ||||
|
解得t=0.
则点P与原点O重合,
∴OF=
| 1 |
| 2 |
∴F(4,0).
点评:本题考查了一次函数综合题.其中涉及到的知识点有:一次函数图象上点的坐标特征,待定系数法求一次函数的解析式,相似三角形的判定与性质等.注意(3)题中构建相似三角形的辅助线的作法.

练习册系列答案
相关题目
已知Rt△ABC中,∠B=90°,三边长a、b、c,那么关于x的方程a(x2-1)-2cx+b(x2+1)=0的根的情况是( )
| A、有两个相等的实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、根的情况不确定 |
 房价(指均价)是人们关心的一个热点问题,已知某市2001年至2011年房价如右统计图,2012、2013年政府准备强行打压,按2009到2011年均价的平均增长率进行下调,已知2005年该市住房总面积为3600万平方米,2007年该市住房总面积为6000万平方米.下列说法:①2001年到2003年均价的平均增长率为10%;②2005年到2007年该市住房总面积平均增长率与均价的平均增长率相同;③预计打压后,2013年均价与2009年均价相同.其中正确的个数有( )
房价(指均价)是人们关心的一个热点问题,已知某市2001年至2011年房价如右统计图,2012、2013年政府准备强行打压,按2009到2011年均价的平均增长率进行下调,已知2005年该市住房总面积为3600万平方米,2007年该市住房总面积为6000万平方米.下列说法:①2001年到2003年均价的平均增长率为10%;②2005年到2007年该市住房总面积平均增长率与均价的平均增长率相同;③预计打压后,2013年均价与2009年均价相同.其中正确的个数有( ) 如图所示,已知在△ABC中,D是BC边上一点,∠1=∠B,∠2=∠C,∠BAC=75°,则∠DAC=
如图所示,已知在△ABC中,D是BC边上一点,∠1=∠B,∠2=∠C,∠BAC=75°,则∠DAC= 如图,梯形ABCD中,AD∥BC,∠C=90°,以AB为直径作⊙O交CD于点E、F,DF=CE,若AB=10,EF=8.
如图,梯形ABCD中,AD∥BC,∠C=90°,以AB为直径作⊙O交CD于点E、F,DF=CE,若AB=10,EF=8. 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).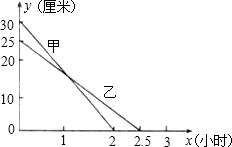 在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间X(小时)之间的关系如图所示.
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间X(小时)之间的关系如图所示. 某校初三年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次,甲、乙两名同学测试情况如图所示.
某校初三年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次,甲、乙两名同学测试情况如图所示.