题目内容
 如图,梯形ABCD中,AD∥BC,∠C=90°,以AB为直径作⊙O交CD于点E、F,DF=CE,若AB=10,EF=8.
如图,梯形ABCD中,AD∥BC,∠C=90°,以AB为直径作⊙O交CD于点E、F,DF=CE,若AB=10,EF=8.求A、B到直线CD的距离之和.
考点:垂径定理,勾股定理,梯形中位线定理
专题:探究型
分析:连接OE,过点O作OG⊥EF于点G,由垂径定理可知GE=
EF=4,由AB=10可知OB=OC=5,再由勾股定理求出OG的长,梯形ABCD中,AD∥BC,∠C=90°,点O是梯形ABCD的中位线,故可得出AD+BC=2OG.
| 1 |
| 2 |
解答: 解:连接OE,过点O作OG⊥EF于点G,
解:连接OE,过点O作OG⊥EF于点G,
∵点O是⊙O的圆心,EF=8,
∴GE=
EF=4,
∵AB=10,
∴OB=OC=5,
∴OG=
=
=3,
∵梯形ABCD中,AD∥BC,∠C=90°,
∴点O是梯形ABCD的中位线,
∴AD+BC=2OG=2×3=6.
答:A、B到直线CD的距离之和是6.
 解:连接OE,过点O作OG⊥EF于点G,
解:连接OE,过点O作OG⊥EF于点G,∵点O是⊙O的圆心,EF=8,
∴GE=
| 1 |
| 2 |
∵AB=10,
∴OB=OC=5,
∴OG=
| OC2-GE2 |
| 52-42 |
∵梯形ABCD中,AD∥BC,∠C=90°,
∴点O是梯形ABCD的中位线,
∴AD+BC=2OG=2×3=6.
答:A、B到直线CD的距离之和是6.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出梯形的中位线是解答此题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠C=90°,AB=5,AC=4,则cosA的值是( )
如图,在△ABC中,∠C=90°,AB=5,AC=4,则cosA的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
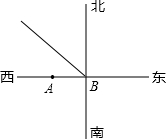 在某岛A的正东方向有台风,且台风中心B距离小岛A40
在某岛A的正东方向有台风,且台风中心B距离小岛A40| 2 |
| A、不受影响 | B、1小时 |
| C、2小时 | D、3小时 |
 如图,以坐标原点为圆心作圆交y轴与点E,AB为⊙O的弦,且AB∥x轴,交y轴于点D,双曲线y=
如图,以坐标原点为圆心作圆交y轴与点E,AB为⊙O的弦,且AB∥x轴,交y轴于点D,双曲线y= =
= 已知:如图梯形ABCD中,AD∥BC,AB=DC,∠B=60°,AD=5cm,BC=9cm.求:
已知:如图梯形ABCD中,AD∥BC,AB=DC,∠B=60°,AD=5cm,BC=9cm.求: