题目内容
19.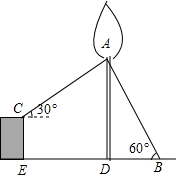 如图,为了固定一棵珍贵的古树AD,在树干A处向地面引钢管AB,与地面夹角为60°,向高CE1.5米的建筑物引钢管AC,与水平面夹角为30°,建筑物CE离古树的距离ED为6米,求钢管AB的长(结果保留整数,参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)
如图,为了固定一棵珍贵的古树AD,在树干A处向地面引钢管AB,与地面夹角为60°,向高CE1.5米的建筑物引钢管AC,与水平面夹角为30°,建筑物CE离古树的距离ED为6米,求钢管AB的长(结果保留整数,参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)
分析 过点C作CF⊥AD于点F,于是得到CF=DE=6,AF=CFtan30°,在Rt△ABD中,根据三角函数的定义即可得到结论.
解答 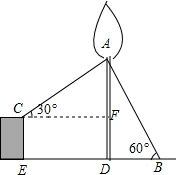 解:过点C作CF⊥AD于点F,则CF=DE=6,AF=CFtan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$.
解:过点C作CF⊥AD于点F,则CF=DE=6,AF=CFtan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$.
∴AD=AF+DF=2$\sqrt{3}$+1.5,
在Rt△ABD中,AB=$\frac{AD}{sin60°}$=(2$\sqrt{3}$+1.5)÷$\frac{\sqrt{3}}{2}$=4+$\sqrt{3}$≈6米.
答:钢管AB的长约为6米.
点评 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度.

练习册系列答案
相关题目
10.用科学记数法记出的数是2.02×10-3,它原来的数是( )
| A. | 0.000202 | B. | 2020 | C. | 0.00202 | D. | 0.0202 |
14.已知x-$\frac{1}{x}=3$,则x2$+\frac{1}{{x}^{2}}$的值是( )
| A. | 9 | B. | 7 | C. | 11 | D. | 不能确定 |
4.计算(-3)+(-2)的结果等于( )
| A. | -5 | B. | 5 | C. | -1 | D. | 1 |
9.下列各式中,正确的是( )
| A. | $\root{3}{-2}$=-$\root{3}{2}$ | B. | -$\sqrt{0.4}$=-0.2 | C. | $\sqrt{(-3)^{2}}$=-3 | D. | $\sqrt{9}$=±3 |
 (1)如图在平行四边形ABCD中,PQ、MN分别平行DC、AD、PQ、MN交于O点,其中S四边形AMOP=3,S四边形MBQO=4,S四边形NCQO=10,则△DMQ的面积=$\frac{17}{2}$.
(1)如图在平行四边形ABCD中,PQ、MN分别平行DC、AD、PQ、MN交于O点,其中S四边形AMOP=3,S四边形MBQO=4,S四边形NCQO=10,则△DMQ的面积=$\frac{17}{2}$.