题目内容
7. (1)如图在平行四边形ABCD中,PQ、MN分别平行DC、AD、PQ、MN交于O点,其中S四边形AMOP=3,S四边形MBQO=4,S四边形NCQO=10,则△DMQ的面积=$\frac{17}{2}$.
(1)如图在平行四边形ABCD中,PQ、MN分别平行DC、AD、PQ、MN交于O点,其中S四边形AMOP=3,S四边形MBQO=4,S四边形NCQO=10,则△DMQ的面积=$\frac{17}{2}$.(2)已知正数a,b,c,d满足$\frac{bcd}{a}$=4,$\frac{acd}{b}$=9,$\frac{abd}{c}$=$\frac{1}{4}$,$\frac{abc}{d}$=$\frac{1}{9}$,则a+c-b-d=-$\frac{5}{6}$.
分析 (1)先根据等高平行四边形的面积比等于底边的比求出平行四边形POND的面积,然后求出三块空白部分的面积,再利用平行四边形ABCD的面积减去空白部分的面积即可;
(2)首先将已知的4个式子相乘得出abcd=1,进而分别求出a,b,c,d的值即可求出答案.
解答 解:(1)设平行四边形POND的面积为x,
则$\frac{x}{3}$=$\frac{10}{4}$,
解得:x=7.5,
S△AMD=$\frac{1}{2}$×(7.5+3)=$\frac{21}{4}$,
S△MBQ=$\frac{1}{2}$×4=2,
S△CDQ=$\frac{1}{2}$×(7.5+10)=$\frac{35}{4}$,
∴三角形区域的面积=3+4+10+7.5-$\frac{21}{4}$-2-$\frac{35}{4}$=$\frac{17}{2}$;
故答案为:$\frac{17}{2}$;
(2)根据题意将四个式子相乘可得:(abcd)2=1,又a,b,c,d为正数,
所以abcd=1,则bcd=$\frac{1}{a}$,又bcd=4a,即$\frac{1}{a}$=4a,
解得a=$\frac{1}{2}$;
则acd=9b,acd=$\frac{1}{b}$,
故9b=$\frac{1}{b}$,
解得:b=$\frac{1}{3}$,
同理可求出:c=2,d=3,
故a+c-b-d=(a+c)-(b+d)=($\frac{1}{2}$+2)-($\frac{1}{3}$+3)=-$\frac{5}{6}$.
故答案为:-$\frac{5}{6}$.
点评 此题主要考查了平行四边形的性质以及分式的混合运算,根据题意正确得出各三角形面积是解题关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
15.计算(-2)+(-4)的结果等于( )
| A. | -2 | B. | 6 | C. | -6 | D. | 8 |
2. 如图,AB∥CD∥EF,若∠ABC=50c,∠CEF=150°,则∠BCE=( )
如图,AB∥CD∥EF,若∠ABC=50c,∠CEF=150°,则∠BCE=( )
 如图,AB∥CD∥EF,若∠ABC=50c,∠CEF=150°,则∠BCE=( )
如图,AB∥CD∥EF,若∠ABC=50c,∠CEF=150°,则∠BCE=( )| A. | 60° | B. | 50° | C. | 30° | D. | 20° |
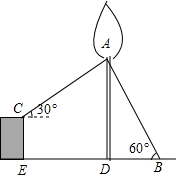 如图,为了固定一棵珍贵的古树AD,在树干A处向地面引钢管AB,与地面夹角为60°,向高CE1.5米的建筑物引钢管AC,与水平面夹角为30°,建筑物CE离古树的距离ED为6米,求钢管AB的长(结果保留整数,参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)
如图,为了固定一棵珍贵的古树AD,在树干A处向地面引钢管AB,与地面夹角为60°,向高CE1.5米的建筑物引钢管AC,与水平面夹角为30°,建筑物CE离古树的距离ED为6米,求钢管AB的长(结果保留整数,参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73) 期末考试后,小红将本班50名学生的数学成绩进行分类统计,得到如图所示的扇形统计图,则该班有10名学生数学成绩为优.
期末考试后,小红将本班50名学生的数学成绩进行分类统计,得到如图所示的扇形统计图,则该班有10名学生数学成绩为优.