题目内容
13．当x=5时，多项式ax3+x-2的值是10，则x=-5时，多项式ax3+x-2的值是（ ）| A． | 14 | B． | 10 | C． | -10 | D． | -14 |
分析 先把x=5代入可求得a的值，也可以求得式子-125a-5=-12，再把x=-5代入得：-125a-5-2，整体代入可得结果．
解答 解：把x=5代入ax3+x-2=10中得：125a+5-2=10，
125a+5=12，
∴-125a-5=-12，
把x=-5代入ax3+x-2中得：-125a-5-2=-12-2=-14，
故选D．
点评 此题主要考查了代数式求值问题，要熟练掌握，求代数式的值可以直接代入、计算，也可以运用整体的思想；本题求a时发现数值较大，不好计算，所以利用了整体代入的思想解决．
练习册系列答案
相关题目
在Rt△ABC中，∠C=90°，若AB=20，AC=16，AD平分∠BAC交BC于点D，且BD：CD=5：4，则点D到线段AB的距离为$\frac{16}{3}$．
4．要使（x2+ax+5）（-6x3）的展开式中不含x4项，则a应等于（ ）
| A． | 1 | B． | -1 | C． | $\frac{1}{6}$ | D． | 0 |
18．下列计算结果中，正确的是（ ）
| A． | （-9）÷（-3）2=1 | B． | （-9）2÷（-32）=-9 | C． | -（-2）3×（-3）2=1 | D． | -（-2）6×（-3）2=-8 |
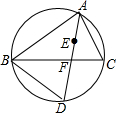如图，点E是△ABC的内心，AE的延长线与BC相交于点F，与△ABC的外接圆相交于点D．