题目内容
7.计算:(1)解不等式,并把解集在数轴上表示出来,$\frac{1-3x}{2}$≥1-2x;
(2)分解因式:a3-4a.
分析 (1)两边同时乘以2去分母,然后再移项、合并同类项即可得解集,再在数轴上表示解集即可;
(2)首先提公因式a,再利用平方差进行二次分解即可.
解答 解:(1)$\frac{1-3x}{2}$≥1-2x,
1-3x≥2-4x,
4x-3x≥2-1,
解得:x≥1,
在数轴上表示为: ;
;
(2)原式=a(a2-4)=a(a+2)(a-2).
点评 此题主要考查了一元一次不等式的解法,以及分解因式,关键是掌握对多项式进行因式分解时,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若x-3是4的平方根,则x的值为( )
| A. | 2 | B. | ±2 | C. | 1或5 | D. | 16 |
17.用分数表示4-2的结果是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
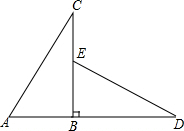 如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么:
如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么: 如图,在△ABC中,已知AB=AC,∠A=40°,DE垂直平分AC交AB于E,求∠BCE的度数.
如图,在△ABC中,已知AB=AC,∠A=40°,DE垂直平分AC交AB于E,求∠BCE的度数.